Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 54a
54. Determine a intensidade dos momentos da força em relação aos eixos x, y e z. Resolva o problema
(a) usando uma abordagem de vetor cartesiano
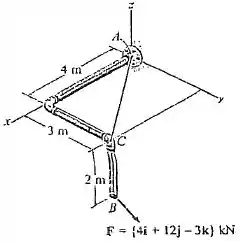
Passo 1
Para fornecer o resultado como o enunciado pede precisamos calcular o momento da força usando o produto vetorial que é dado da seguinte maneira:
Onde:
representam as componentes do vetor unitário definido na direção do eixo de rotação
representam as coordenadas do vetor posição definido a partir de qualquer ponto O sobre o eixo de rotação até qualquer ponto na linha de aplicação da força.
são as componentes da força aplicada.
Teremos que fazer essa abordagem para cada caso de eixo de rotação. Então vamos resolver cada um separadamente.
Passo 2
Começando com o eixo x como eixo de rotação.
O vetor para essa situação pode ser visto na figura abaixo.
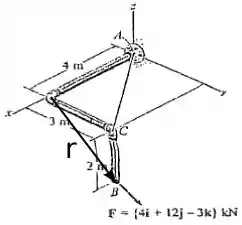
Para saber as coordenadas desse vetor, basta olhar a figura e ver quanto você tem que andar para cada direção para chegar ao ponto na linha de ação da força, logo:
O vetor unitário que tem a mesma direção que o eixo de rotação que é o eixo x, é dado por:
Passo 3
Agora que já temos tudo que precisamos, vamos calcular o momento em relação ao eixo pedido.
Passo 4
Agora com o eixo y como eixo de rotação.
O vetor para essa situação pode ser visto na figura abaixo.
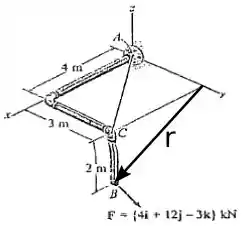
Para saber as coordenadas desse vetor, basta olhar a figura e ver quanto você tem que andar para cada direção para chegar ao ponto na linha de ação da força, logo:
O vetor unitário que tem a mesma direção que o eixo de rotação que é o eixo y, é dado por:
Passo 5
Agora que já temos tudo que precisamos, vamos calcular o momento em relação ao eixo pedido.
Passo 6
Agora com o eixo z como eixo de rotação.
O vetor para essa situação pode ser visto na figura abaixo.
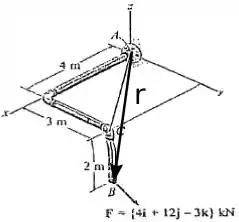
Para saber as coordenadas desse vetor, basta olhar a figura e ver quanto você tem que andar para cada direção para chegar ao ponto na linha de ação da força, logo:
O vetor unitário que tem a mesma direção que o eixo de rotação que é o eixo z, é dado por:
Passo 7
Agora que já temos tudo que precisamos, vamos calcular o momento em relação ao eixo pedido.
Resposta
A intensidade dos momentos da força em relação aos eixos x, y e z são: