Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 87
Se a corda possui de comprimento, determine a posição da coordenada do ponto .
Passo 1
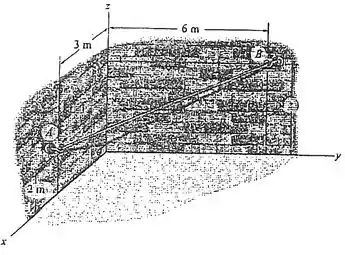
Fala! Nessa questão queremos a coordenada do nosso ponto , e para achar isso temos as outras coordenadas desse ponto, as coordenadas de e comprimento de . Como a gente pode relacionar o que tem com , para acha ele?
Cara, pensa comigo: a partir das coordenadas de e a gente pode achar um vetor que liga esses pontos. Calculando o módulo desse cara, a gente acha o comprimento desse segmento.
Como a gente já tem esse comprimento, esse módulo na real vai ser uma equaçãozinha para achar . Bora lá!
Vamos começar encontrando as coordenadas dos pontos e pondo nossa incógnita no local correto:
Definimos nosso vetor que sai de e vai para fazendo o ponto final menos inicial, assim:
Passo 2
Aí a gente calcula o módulo desse vetor:
Mas a gente já sabe quando o módulo vale, porque ele é igual ao comprimento da corda dado pelo enunciado, então vamos substituir ele aqui junto com as nossas coordenadas do vetor:
Agora é isolar
Como o exercício determina nossa posição como positivo, então: