Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 68

Determine a localização e do centro de cisalhamento (ponto O ) para o elemento de paredes finas com a seção transversal mostrada na figura, onde b 2 > b 1 . Os segmentos do elemento têm a mesma espessura t .

Passo 1

Observe a distribuição de forças geradas sobre a viga. Elas vão gerar um momento sobre a viga e isso gera uma “torção na viga”

O centro de cisalhamento é o ponto O onde uma força P aplicada, gera um momento equivalente ao das forças internas, anulando a torção.

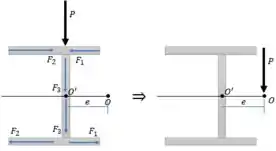
Pra calcular isso, vamos integrar o fluxo de cisalhamento sobre a viga para determinar as forças internas em função de P . Depois vamos fazer um cálculo de momento equivalente, para determinar a distância e .

Como já conhecemos a força que atua no ponto O, então vamos fazer este cálculo de momentos em relação ao ponto O ' . Dessa forma não vamos precisar calcular a força F 3 .

Passo 2

Começamos calculando o momento de inércia:

I = 1 12 t h 3 + 2 b 1 + b 2 t h 2 2

I = t h 2 12 ( h + 6 b 1 + 6 b 2 )

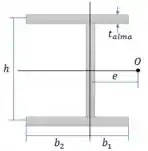
Passo 3

Na figura está destacado o comportamento do momento estático nas abas. Vamos usar isso para determinar uma equação para o momento estático nas abas

Q 1 = x 1 ⋅ t ⋅ h 2 ,   o n d e   0 < x 1 < b 1

Q 2 = x 2 ⋅ t ⋅ h 2 ,   o n d e   0 < x 2 < b 2

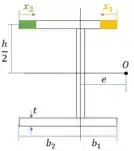
Passo 4

Agora vamos calcular as forças. Basta integrar o fluxo de cisalhamento na região:

Força 1:

F 1 = ∫ 0 b 1 q 1 d x = ∫ 0 b 1 V Q 1 I d x

F 1 = V I ∫ 0 b 1 x 1 ⋅ t ⋅ h 2 d x

F 1 = P t h 2 I ⋅ x 1 2 2 0 b 1

F 1 = P t h 4 I ⋅ b 1 2

Força 2: Observe que para a força 2 temos a mesma integral:

F 2 = ∫ 0 b 2 q 2 d x = ∫ 0 b 2 V Q 2 I d x

F 2 = P t h 4 I ⋅ b 2 2

Passo 5

Agora vamos imaginar que aplicamos a força P no centro de cisalhamento O , nesse caso, por definição,

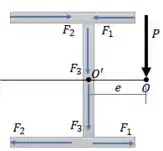
A F 1 e a F 2   geram binários com braço h :

∑ M O ' = 0 ⇒ - F 2 ⋅ h + F 1 ⋅ h + P ⋅ e = 0

e = h P ( F 2 - F 1 )

e = h P P t h 4 I ⋅ b 2 2 - P t h 4 I ⋅ b 1 2

e = t h 2 4 I b 2 2 - b 1 2

e = t h 2 4 t h 2 12 h + 6 b 1 + 6 b 2   b 2 2 - b 1 2

e = 3 h + 6 b 1 + 6 b 2   b 2 2 - b 1 2

e = 3 b 2 2 - b 1 2 h + 6 ( b 1 + b 2 )  

Resposta

e = 3 b 2 2 - b 1 2 h + 6 ( b 1 + b 2 )  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três forças são aplicadas a um perfil de aço laminado W250 X 49,1, como mostrado. Determinar as tensões normal e de cisalhamento nos pontos A e B.
Três forças são aplicadas a um perfil de aço laminado W250 X 49,1, como mostrado. Determinar as tensões normal e de cisalhamento nos pontos C e D.
Três placas de aço, cada uma com 12,5 mm de espessura, são soldadas juntas para formar uma viga em balanço. Para o carregamento mostrado, determinar as tensões normal e de cisalhamento nos pontos D e
Uma força de 12 kN é aplicada à extremidade livre da viga em balanço AB, na direção perpendicular ao eixo longitudinal da viga. Determinar a tensão no ponto A para quando o ângulo é 0 e para quando é
Uma força P de 5k N é aplicada a um arame, que é enrolado em torno da barra A B , como mostrado. Sabendo-se que a seção transversal da barra é um quadro de lado d = 40m m , determinar a tensão de cisa