Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 44

A viga-mestra de alma dupla é composta por duas folhas de compensado presas a elementos de madeira na parte superior e na parte inferior. A tensão de flexão admissível para a madeira é σ a d m = 56   M P a , e a tensão de cisalhamento admissível é τ a d m = 21   M P a . Se os elementos de fixação forem espaçados de s = 150 m m e cada um puder suportar 3   k N em cisalhamento simples, determine a carga máxima P que pode ser aplicada à viga.

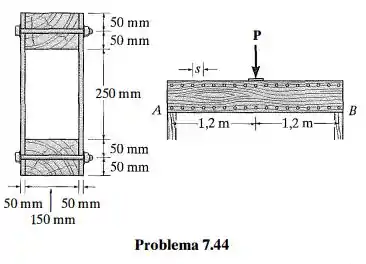
Passo 1

Dados da questão: σ a d m = 56   M P a ,   τ a d m = 21   M P a ,   s = 150   m m ,   F p a r a f u s o = 3 k N ,   L = 2,4   m

A questão pede a carga P = ?

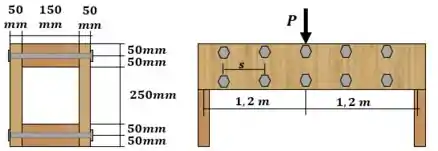
Primeiro vamos calcular as reações de apoio e determinar os esforços internos na viga.

Segundo vamos calcular as propriedades geométricas da seção transversal: Momento de Inércia e Momento Estático. Como a seção é perfeitamente simétrica, o centroide é no centro.

Depois, usaremos as equações de fluxo de cisalhamento para determinar a carga P.

Passo 2

Fazemos um diagrama de corpo livre

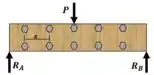
É uma viga simplesmente apoiada com carga centralizada e reações simétricas, então podemos garantir que:

R A = R B = P 2

Observe que para uma viga simplesmente apoiada o diagrama de esforço cortante é:

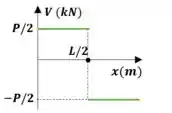
Passo 3

Vamos calcular agora o momento de inércia:

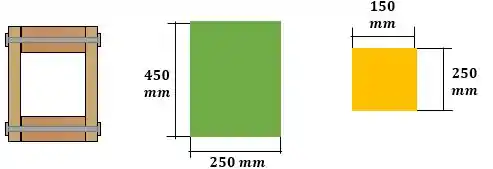
Podemos calcular o momento de inércia, subtraindo o momento de inércia verde do amarelo

I = I v e r d e - I a m a r e l o

I = 250 ⋅ 450 3 - 150 ⋅ 250 3 12

I = 1,7 ⋅ 10 9   m m 4

Passo 4

Por simplicidade, vamos escolher uma das madeiras do meio para fazer o momento estático

Q = A ⋅ y

Q = ( 150 ⋅ 100 ) ⋅ 175

Q = 2625000   m m 3

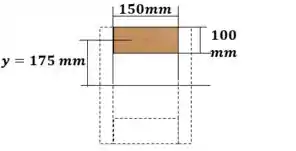
Passo 5

Observe a figura abaixo. Perceba que a seção que selecionamos está em contato com duas chapas laterais, e gerando um cisalhamento duplo sobre o parafuso. A relação entre o parafuso e fluxo de cisalhamento é:

q = 2 F p a r a f u s o s

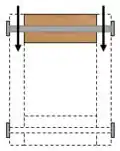
O número dois aparece na equação acima, pois o parafuso está em cisalhamento duplo.

Por outro lado, a fórmula para o fluxo de cisalhamento é

q = V ⋅ Q I

Igualando as duas equações:

V ⋅ Q I = 2 F p a r a f u s o s

Isolando V :

V = 2 F p a r a f u s o ⋅ I s ⋅ Q

Substituindo o valor do esforço cortante:

P 2 = 2 ⋅ F p a r a f u s o ⋅ I s ⋅ Q

P = 4 ⋅ F p a r a f u s o ⋅ I s ⋅ Q

P = 4 ⋅ 3 k N ⋅ 1,7 ⋅ 10 9   m m 4 150   m m ⋅ 2625000   m m 3

P = 51,81   k N

Resposta

P = 51,81   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a posição e para a aplicação da força P de modo que a viga sofra deflexão para baixo sem torção. Considere h = 200m m .
Determine a localização e do centro de cisalhamento (ponto O) para o tubo que tem uma fenda ao longo de seu comprimento
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura.
A força P é aplicada à alma da viga como mostra a figura. Se e = 250 m m , determine a altura h da aba direita de modo que a viga sofra deflexão para baixo sem torção. Os segmentos do elemento têm a m
A viga é composta por quatro tábuas pregadas como ostra a figura. Determine a força de cisalhamento à qual cada prego ao longo dos lados C e da parte superior D deve resistir se estiverem uniformement