Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 70
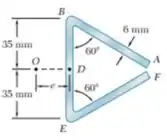
Determine a localização do centro de cisalhamento de uma viga de paredes finas de espessura uniforme com o seção transversal mostrada.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a localização do centro do centro de cisalhamento de uma viga de paredes finas de espessura uniforme. Para isso vamos começar esboçando o diagrama de corpo livre :D.
Vamos começar a determinar a inércia do elemento, então partiu!
Considerando os dados
Passo 2
Considerando a área
E o ângulo de 30° temos:
Fazendo o somatório do momento em D podemos determinar a localização do centro de cisalhamento
Resposta
20,2 mm
Exercícios de Livros Relacionados
Uma barra com a seção transversal mostrada na figura foi construída unindo-se firmemente latão e alumínio. Usando os dados fornecidos abaixo, determine o maior momento fletor admissível quando a barra
Vigas de madeira e chapas de aço são aparafusadas firmemente para formar o elemento composto mostrado na figura. Usando os dados da tabela abaixo, determine o maior momento fletor admissível quando a
Uma barra com a seção transversal mostrada na figura foi construída unindo-se firmemente latão e alumínio. Usando os dados fornecidos abaixo, determine o maior momento fletor admissível quando a barra
Para a barra composta indicada, determine o maior momento fletor admissível quando a barra é flexionada em torno do eixo vertical. Barra do problema 4.3 4 .
Vigas de madeira e chapas de aço são aparafusadas firmemente para formar o elemento composto mostrado na figura. Usando os dados da tabela abaixo, determine o maior momento fletor admissível quando a