Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 19

Determine a localização x - do centroide C da parte superior da cardioide, r = a ( 1 - cos ⁡ θ ) .

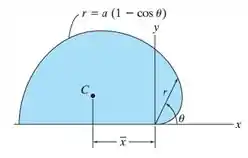
Passo 1

Vamos tomar nosso Elemento Diferencial como a área em cinza mostrada na figura:

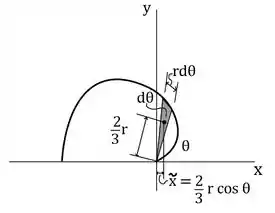
Para isso, essa área é dada por:

ⅆ A = 1 2 r 2 ⅆ θ

Essa relação é padrão para coordenadas polares.

Passo 2

Vamos então encontrar nossa área com os limites de integração de 0 até π já que estamos estudando a parte superior da cardioide:

A = ∫ A ⅆ A

A = ∫ 0 π 1 2 a 2 1 - cos ⁡ θ 2 ⅆ θ = 3 4 π a 2

Passo 3

E agora encontramos nosso centroide x - :

x - = ∫ A x - ⅆ A ∫ A ⅆ A

Temos que:

∫ A x - d A = ∫ 0 π 2 3 r cos ⁡ θ 1 2 a 2 1 - cos ⁡ θ 2 ⅆ θ

= 2 6 a 3 ∫ 0 π cos ⁡ θ 1 - cos ⁡ θ 3 ⅆ θ = - 1,9635 a 3

Então:

x - = - 1,9635 3 4 π a 2 = - 0,833 a

Resposta

x - = - 0,833 a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide x ¯ da área.
Localize o centroide y ¯ da área.
Localize o centroide z ¯ do segmento esférico.
Determine a localização z ¯ do centroide para o tetraedro. Sugestão: use um elemento de “placa” triangular paralelo ao plano x – y e de espessura d z .
Localize o centroide do quarto de cone.