Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 47
Determine a localização do centroide para o tetraedro. Sugestão: use um elemento de “placa” triangular paralelo ao plano e de espessura .
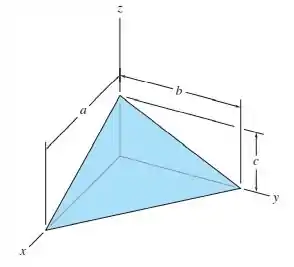
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão de Estática.
Este problema nos pede para determinarmos o centroide do sólido da figura. Sabemos que ele é dado por:
Primeiro, devemos determinar a posição do centro de massa do sólido. A partir da equação do plano, temos:
Assim, temos que as posições e do centro de massa vão ser, respectivamente:
Passo 2
Em seguida, vamos determinar a posição do centroide. Para isso, basta encontramos a integral que corresponde ao numerador da equação do centroide e dividirmos pelo volume. Fica assim:
É isso, galera, Bora resolver mais questões pra ficar craque.