Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 83
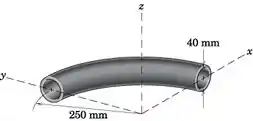
Determine a massa do comprimento de um quarto de círculo da mangueira do radiador. O diâmetro interno é 40 mm, a espessura da parede é 4 mm e a densidade do material de borracha é 1050 kg / m3.
Passo 1
O volume desta concha toroidal de um quarto é, pelo Teorema de Pappus, o volume varrido pelo anel plano quando girado em torno do eixo z em .
Passo 2
Agora, massa = densidade x volume.
Portanto
Resposta
Exercícios de Livros Relacionados
65. A placa composta é feita de segmentos de aço A e bronze B . Determine a massa e a localização x - , y - , z - de seu centro de massa G. Considere ρ a ç o = 7,85M g / m 3 ç e ρ b r = 8,74M g / m 3
Localize o centroide y - da área da secção transversal da viga construida.
Divida a placa em partes e, usando a grade para medição, determine aproximadamente a localização ( x - , y - ) do centróide da placa.
Para determinar a localização do centro de gravidade do automóvel, ele primeiro é colocado em uma posição nivelada, com as duas rodas em um lado apoiando sobre a plataforma P de uma balança. Nessa pos
Localize o centroide ( x - ,y - ) da área composta.