Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 61
Divida a placa em partes e, usando a grade para medição, determine aproximadamente a localização () do centróide da placa.
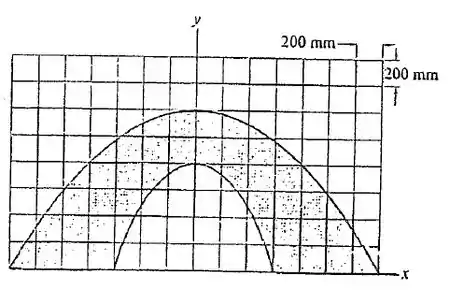
Passo 1
O problema pede que encontremos o centroide da área, como você já deve saber é calculada por:
Nós vamos dividir nossa região em áreas menores e mais simples.
Bom galera, por sorte a gente percebe que a figura é simétrica em relação a . Isso nos dá duas vantagens
- a coordenada do centroide está no eixo de simetria, logo temos que
- podemos calcular a coordenada em relação somente a metade dessa figura, aí diminui bastante nosso trabalho, né?
Passo 2
Beleza, agora a gente vai tentar simplicar a metade da figura usando triângulos e quadrados, só precisamos da metade que é simétrica a outra, bem assim:
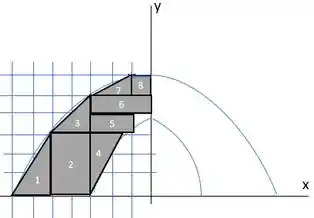
Nós vamos medir de cada uma dessas figuras, lembrando que o lado de cada quadradinho azul desse vale 200 mm.
Para os retângulos, vai ser o valor de até chegar na sua base mais metade da sua altura. E para os triângulos 1,7 e 3, vai ser o valor de até chegar a sua base mais um terço da sua altura. E para , vai ser dois terços da sua altura (já que sua ponta está coladinha em ).
Por que? Porque o centroide do triângulo está a um terço da base desse triângulo. E para o retângulo, ele está no meio.
Passo 3
Com isso, a gente monta uma tabelinha com a área e o de cada figurinha, e os somatórios:
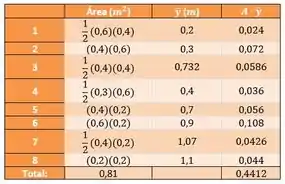
Passo 4
Agora a gente só usa a formula:
Em milímetros fica:
Então: