Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas - Ex. 59
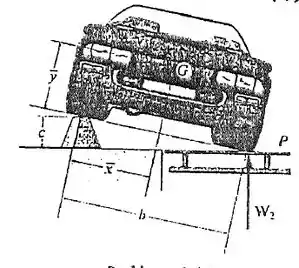
Para determinar a localização do centro de gravidade do automóvel, ele primeiro é colocado em uma posição nivelada, com as duas rodas em um lado apoiando sobre a plataforma de uma balança. Nessa posição, a balança registra uma leitura de . Depois, um lado é elevado para uma altura conveniente , conforme mostra a figura. A nova leitura na escala é . Se o automóvel tem um peso total de , determine a localização de seu centro de gravidade ().
Passo 1
O problema pede que encontremos o centro de gravidade do carro. E nos dá duas situações. A ideia aqui é a gente usar o fato de que a resultante do peso do carro está localizado no centro de gravidade e que o carro está em equilíbrio nas duas situações.
A partir das equações de equilíbrio das duas situações, podemos achar as coordenadas de .
Então vamos analisar um pouco quando o carro está nivelado:
A gente pode usar o momento para ver o que a gente encontra sobre as forças de reação na roda do carro, então vamos usar a equação de equilíbrio do momento, tendo como eixo de rotação o ponto , considerando o sentido horário positivo
Logo:
Repara que já achamos ! Vamos seguir!
Passo 2
Beleza, agora a gente vai analisar quando o carro estiver inclinado.
Precisamos dos senos e cossenos do ângulo de inclinação para conseguir fazer as equações de equilíbrio da situação inclinada, já que vamos precisar decompor umas coisinhas em relação ao eixos vertical e horizontal.
Temos esse triângulo na figura, usando Pitagoras para completar o lado que falta:
Assim a gente percebe que:
Passo 3
Agora a gente faz o diagrama de corpo livre com o carro inclinado:
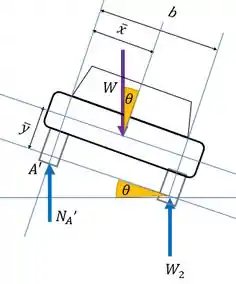
E denovo a gente usa a equação de equilíbrio pro momento no ponto . Repara que o que está inclinado, a gente vai decompor nos eixos vertical e horizontal, para ter os braços de alavanca certinho de cada força.