Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 60
Localize o centroide () da área composta.
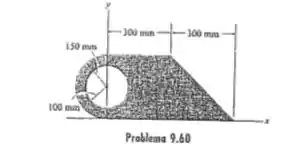
Passo 1
Fala galera boa, tudo belezinha com vocês?! Bora resolver esse exercício aqui!
O problema pede que encontremos o centroide da área da figura composta, então pra isso podemos usar as equações:
Iradoso, então podemos dividir nossa figura em partes como no esquema a seguir:
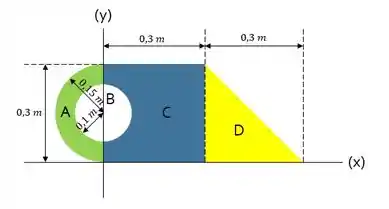
Onde é a semicircunferência de raio de e é uma circunferência de raio e área negativa!
Passo 2
Beleza, agora a gente vai calcular a aréa de cada um dos segmentos:
Vamos considerar negativo porque é uma área que falta.
Passo 3
Show de bolinhas, então agora podemos montar uma tabelinha com as componentes e de cada figura, e também podemos incluir os valores de e , logo:
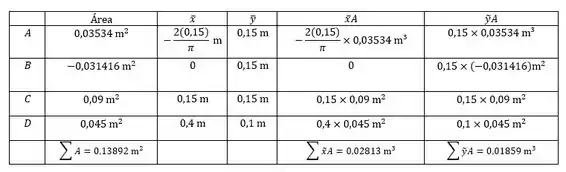
Sendo assim, vamos obter que a componente será:
Segue que:
Passando para :
E agora para o a componente :
De modo que:
Passando para :
Portanto as coordenadas do centroide será: