Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 204
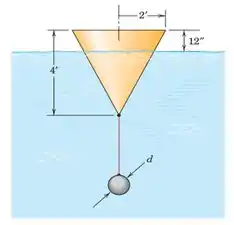
A superfície cônica e a base circular da bóia de água salgada são fabricadas em uma placa de aço fina que pesa 10,2 libras por pé quadrado. Calcule o diâmetro d da bola esférica de chumbo suspensa no vértice da bóia para que a base será de 12 pol. acima da superfície da água.
Passo 1
E ai gurizada tudo belezinha???
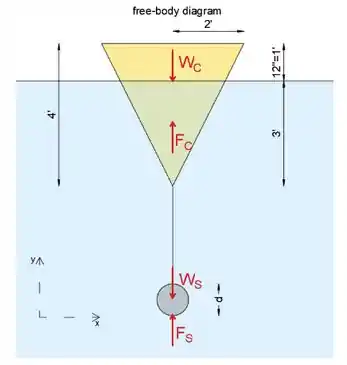
Primeiro, isolaremos e desenharemos o diagrama de corpo livre do cone e da esfera com seus pesos e forças de flutuabilidade atuando em ambas as figuras.
Se o cone é sagrado, teremos que calcular sua superfície para determinar seu peso.
Onde é o comprimento do lado do cone. Substitua r e L por seus valores na expressão acima.
Como o peso do local de aço (do qual o cone é modo) é , o peso do cone é:
Para escrever a expressão para o peso da esfera, teremos que calcular seu volume.
Observe que o peso específico do chumbo é o peso da esfera é:
Passo 2
Primeiro, isolaremos o diagrama de corpo livre do cone e da esfera com seus pesos e forças de flutuabilidade atuando em ambas as figuras.
A força de empuxo é igual ao peso e volume específicos da água.
O volume do cone sob a água é:
Imagine que cortamos o cone ao nível do mar. Usar o raio de proporção de um círculo cortado é:
Substitua r por seus valores na expressão para o volume do cone.
Como o volume de uma esfera já foi calculado na etapa acima, podemos substituir V e por seus valores na expressão de F para calcular as forças de empuxo que atuam no cone e na esfera.
Passo 3
Equacionando a soma das forças na direção y a zero, obteremos a equação em que a dimensão d é a única incógnita.
Substitua todas as forças por expressões escritas nas etapas anteriores.
A partir daqui, podemos expressar d como: