Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 40
Se , determine o menor coeficiente de atrito estático entre A e B de modo que o rolete permaneça preso, independente da intensidade da força P aplicada à correia. Despreze o peso do cilindro e o atrito entre a correia e a superfície vertical.
Passo 1
Desenhando o diagrama do corpo livre:
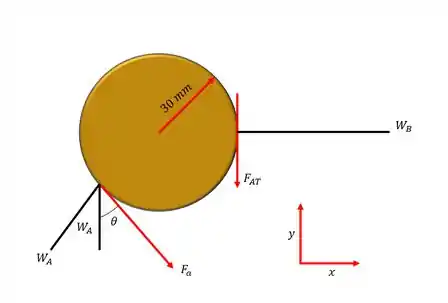
Passo 2
Vamos definir e como os coeficientes de atrito em A e B respectivamente.
Na iminência de deslizar, a força de atrito máxima em B é:
Passo 3
Podemos iniciar calculando o equilíbrio em relação ao momento no ponto A:
Passo 4
Aplicando as equações do equilíbrio no eixo x:
Passo 5
Aplicando as equações do equilíbrio no eixo y:
Passo 6
Substituindo em :
Resposta
Exercícios de Livros Relacionados
A haste esbelta AB de comprimento l = 600m m é ligada a um colar em B e repousa sobre um pequeno rolete localizado a uma distância horizontal a = 80m m da barra vertical sobre a qual o colar desliza.
Duas barras idênticas de 1,5 m de comprimento conectadas por um pino em B estão colocadas entre duas paredes e uma superfície horizontal como mostrado na figur. Designando por μ s o coeficiente de atr
Dois blocos A e B de 8 kg repousam em prateleiras e são conectadas por uma barra de massa desprezível. Sabendo que a intensidade da força P aplicada em C é lentamente incrementada a partir de zero, de
Duas hastes esbeltas de peso desprezível são conectadas por um pino em C e ligadas aos blocos A e B, cada qual com peso W. Sabendo que θ = 80 ° e que o coeficiente de atrito estático entre os blocos e
Uma barra esbelta de aço de 22,5 cm de comprimento é colocada dentro de um tubo, tal como mostra a figura. Sabendo que o coeficiente de atrito estático entre a barra e o tubo é 0,20; determine o maior