Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 37
Se o coeficiente de atrito estático entre a corrente e o plano inclinado é , determine o comprimento pendurado b de modo que a corrente esteja prestes a deslizar plano acima. A corrente pesa w por unidade de comprimento.
Passo 1
Desenhando o diagrama de corpo livre simplificado do problema:
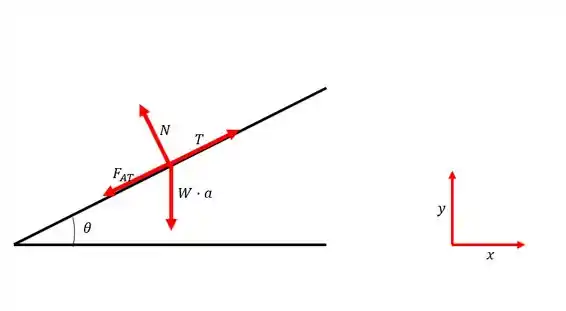
Passo 2
Podemos começar escrevendo o valor da tensão :
Passo 3
Como a corrente está na iminência de escorregar, podemos escrever:
Passo 4
Aplicando as equações do equilíbrio nos eixos x e y:
Resposta
Exercícios de Livros Relacionados
Dois blocos A e B de 4,5 N estão ligados por uma haste esbelta de massa desprezível. O coeficiente de atrito estático é 0,30 entre todas as superfícies de contato, e a barra forma um ângulo θ = 30 ° c
Sabendo que o coeficiente de atrito estático entre o colar e a barra é 0,40, determine o intervalo dos valores de M para que o equilíbrio seja mantido quando θ = 6 0 ° e P = 200N .
Uma viga de 3 m, pesando 5400 N, é movida para a esquerda sobre a plataforma. A força horizontal P é aplicada no carrinho, que é montado em rodas sem atrito. Os coeficientes de atrito entre as superfí
Duas tábuas uniformes idênticas, cada qual pesando 180 N, estão encostadas temporariamente uma contra a outra tal como mostra a figura. Sabendo que o coeficiente de atrito estático entre todas as supe
( a ) Mostre que a viga do Problema 8.34 não pode se mover se a superfície superior do carrinho é ligeiramente mais baixa que a plataforma. ( b ) Mostre que a viga pode ser movida se dois trabalhadore