Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 73
Determine o menor diâmetro admissível do eixo que está sujeita às forças concentradas. Os mancais de luva em e suportam somente forças verticais, e a tensão de flexão admissível é .
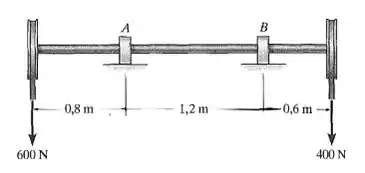
Passo 1
Aplicando-se as equações de equilíbrio, podemos encontrar as reações de apoio.
Podemos então fazer o diagrama:
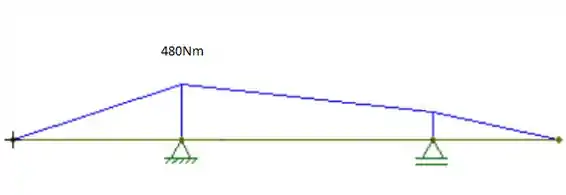
Passo 2
O momento máximo é de 480Nm. Logo, podemos calcular a distância da linha neutra, que será o raio:
Resposta
Exercícios de Livros Relacionados
Uma barra de seção transversal quadrada, como indicado, é feita de um aço que é considerado ser elastoplástico com E = 200G P a e σ e = 240M P a . Determinar o momento fletor M , para que: (a) ocorra
A barra A B é feita de um aço que é considerado ser elastoplástico com E = 200G P a e σ e = 240M P a . Determinar o momento fletor M , para que o raio de curvatura da barra seja: (a) 18m
Uma barra de seção transversal quadrada, como indicado, é feita de um aço que é considerado ser elastoplástico com E = 200G P a e σ e = 300M P a . Determinar o momento fletor M , para que: (a) ocorra
A barra A B é feita de um aço que é considerado ser elastoplástico com E = 200G P a e σ e = 240M P a . Determinar o momento fletor M , para que o raio de curvatura da barra seja: (b) 9m
Uma barra prismática AB é feita de um aço que considerado ser elastoplásticos com E =200 GPa e σ e = 250M P a . Sabendo-se que M = 450N m , determinar (a) a espessura do núcleo elático (b) o raio de c