Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 53

A viga é composta por quatro tábuas pregadas. Se os pregos estiverem de ambos os lados da viga e cada um puder resistir a um cisalhamento de 3   k N , determine a carga máxima P que pode ser aplica à extremidade da viga

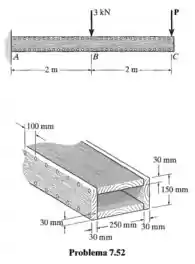
Passo 1

Dados da questão: τ p r e g o = 3 k N ,   s = 100 m m ,   d = 5 m m

A questão pede o carregamento sobre a viga: P = ?

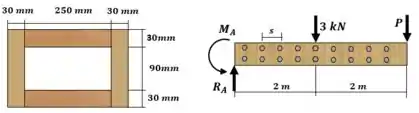
Estratégia de resolução: Vamos começar calculando as reações de apoio no ponto A. Observe que o ponto A será o ponto de maior esforço cortante interno.

Depois poderemos definir o momento de inércia da seção transversal. Não é preciso calcular o centroide, pois a seção transversal é perfeitamente simétrica, e por isso seu centroide é no seu centro.

Após isso podemos usar a equação de fluxo de cisalhamento para definir as forças interna máxima, e consequentemente a carga P

Passo 2

Calculando as reações de apoio:

∑ F y = 0 ⇒ R A - 3 - P = 0

R A = 3 + P

∑ M A = 0 ⇒ M A - 3 ⋅ 2 - P ⋅ 4 = 0

M A = 6 + 4 P

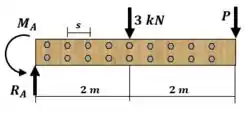
Como o ponto A é o ponto de maior esforço interno, então: V = 3 + P

Passo 3

Agora podemos calcular o momento de inércia. Podemos simplesmente calcular o momento de inércia de um retângulo sólido e subtrair o momento de inércia correspondente ao retângulo vazio

I = 310 ⋅ 150 3 12 - 250 ⋅ 90 3 12 = 72 ⋅ 10 6 m m 4

I = 72 ⋅ 10 - 6 m 4

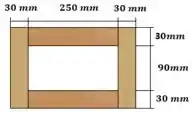
Passo 4

Mas antes de podermos aplicar a equação de fluxo de cisalhamento, precisamos calcular o momento estático na região dos pregos. A região escolhida esta destacada:

Q = 250 ⋅ 30 ⋅ 60 = 450000 m m 3

Q = 45 ⋅ 10 - 5 m 3

Passo 5

Perceba que a seção que selecionamos está em contato com duas chapas laterais, e gerando um cisalhamento sobre dois pregos. A relação entre o prego e fluxo de cisalhamento é:

q = 2 F p r e g o s

O número dois aparece na equação acima pois há dois pregos sobre o mesmo fluxo de cisalhamento.

Por outro lado, a fórmula para o fluxo de cisalhamento é

q = V ⋅ Q I

Igualando as duas equações:

V ⋅ Q I = 2 F p r e g o s

Isolando V

V = 2 F p r e g o ⋅ I Q ⋅ s

Substituindo   V :

3 k N + P = 2 F p r e g o ⋅ I Q ⋅ s

Substituindo os valores:

P =   2 ⋅ 3 k N ⋅ 72 ⋅ 10 - 6 m 4 45 ⋅ 10 - 5 m 3 ⋅ 0,1 m - 3 k N

P = 6,6   k N

Resposta

P = 6,6   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga com avanço foi construída com duas peças de madeira de 50 mm por 100 mm escoradas como mostra a figura. Se a tensão de flexão admissível for σ a d m = 4,2M P a , determine a maior carga P que p
Determine a variação do raio r da viga em balanço que suporta a carga distribuída uniforme, de modo que ela tenha uma tensão de flexão máxima constante σ m á x á em todo o seu comprimento.
A viga tem largura w e altura que varia como mostra a figura. Se ela suportar uma força concentrada P em sua extremidade, determine a tensão de flexão máxima absoluta na viga e especifique sua localiz
A viga tem a forma de um tronco de cone reto com diâmetro de 12 mm em A e de 300 mm em B. Se ela suportar uma força de 750 N em A, determine a tensão de flexão máxima absoluta na viga e especifique su
Selecione no apêndice B a viga de abas largas de aço que tenha o menor peso e que suportará com segurança as cargas mostradas. A tensão de flexão admissível é σ = 160M P a e a tensão de cisalhamento a