Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 75
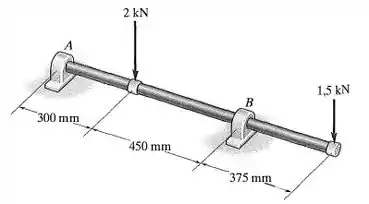
Determine o menor diâmetro admissível para o eixo que está sujeito às forças concentradas. Os mancais de luva em e suportam somente forças verticais, e a tensão de flexão admissível é .
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat. Primeiro, vamos fazer o DCL (diagrama de corpo livre):
Passo 2
Em seguida, vamos encontrar as forças e a partir da condição de equilíbrio no eixo e de momento.
Vamos começar olhando o somatório dos momentos sobre o ponto , pois assim sumimos com uma incógnita ()...
Considerando o sentido anti-horário como positivo, teremos:
Da onde encontramos nossa reação em ....
E para calcular , o jeito mais rápido é fazendo o somatório das forças em ... vou considerar para cima como positivo aqui.
Show, já sabemos todas as nossas forças, agora precisamos encontrar o nosso momento fletor para cada seção...
Passo 3
Para encontrar a equação do momento fletor (), é necessário fazer o balanço do momento em cada seção (que vão de 0 até x metros), ou seja:
(Lembre sempre de verificar se vai ser anti-horário (+) ou horário (-), tá bem?)
Então vem comigo para encontrarmos o momento ;)
Seção 1:
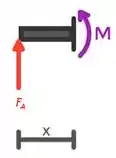
E essa seção vai até , por isso o valor limite nessa seção é:
Seção 2:
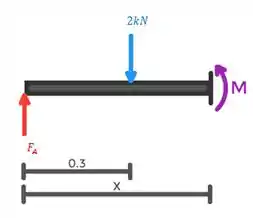
E essa seção vai até , por isso o valor limite nessa seção é:
Perceba que nosso momento era positivo na seção 1 e se tornou negativo em algum ponto aqui na seção 2, para desenhar um bom gráfico, vamos analisar em qual ponto o momento passou de positivo para negativo, isso é, em qual ponto o momento foi zero.
Seção 3:
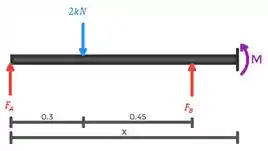
E essa seção vai até , por isso o valor limite nessa seção é:
Agora vamos desenhar o diagrama para fica fofinho :D
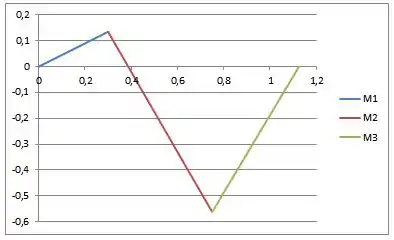
Para montar esse gráfico, eu usei as equações que encontramos para o em cada seção. Aqui eu pude usar o excel e ficou tudo fácil, mas pode ser que você tenha que montar um gráfico assim traçando as retas que encontramos.
Repara só que o ponto de momento máximo em módulo ocorre na passagem entre a seção 2 e a seção 3 e esse valor a gente já calculou, ele é:
No SI, teremos:
Gurizada agora que encontramos o momento máximo, vamos aplicar na equação da tensão normal máxima, a qual o nosso eixo precisa suportar:
Nesse caso, é a distância máxima em relação a linha neutra... Para uma seção transversal circular, essa distância vai ser o próprio raio da seção...
e o momento de inércia de uma área circular é:
Substituindo...
Substituindo os valores...
Por fim, basta lembrarmos da seguinte fórmula para encontrarmos o diâmetro. Temos:
Aeeeeeeeee superamos !!!!!!