Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas de Revisão - Ex. 162
Para a viga e o carregamento mostrados na figura, determine a reação em , a deflexão no ponto . Utilize .
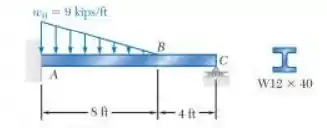
Passo 1
Fala aí, galera. Beleza? Vamos praticar mais mecânica pra tirar aquele na prova.
Primeiro, vamos determinar a reação em :
E também:
Para determinarmos o que é pedido, vamos utilizar a seguinte relação:
Ela nos diz que a derivada da função de força cortante é a função simétrica da função do carregamento distribuída. Dado que o carregamento é dado por:
Podemos obter a equação de momento integrando esta equação duas vezes:
Essa a equação de momento.
Passo 2
Com isso, podemos substituir a equação de momento que encontramos na equação diferencial da linha elástica. Ela é dada por:
Substituindo:
Agora, considerando a rigidez à flexão constante, vamos integrar esta equação duas vezes, para obtermos, respectivamente, a equação para a força cortante e a equação da linha elástica. Integrando, temos:
Integrando mais uma vez:
Passo 3
Em seguida, precisamos encontrar a equação da linha elástica. Para isso, vamos encontrar as condições de contorno para as equações do ultimo passo. Fica assim:
Portanto:
Com as constantes definidas, basta as substituirmos nas equações que encontramos anteriormente. A equação da linha elástica vai ser:
E a equação para a inclinação vamos encontrar substituindo a constante em . Logo:
Passo 4
Para encontrarmos a reação em , temos:
Substituindo:
Opa, encontramos a reação em .
Passo 5
Por fim, para encontrarmos a deflexão no ponto , vamos resolver a equação da linha elástica neste ponto. Temos:
Substituindo: