Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 126
Determine o momento associado ao par de forças de 400 N aplicado à estrutura em .
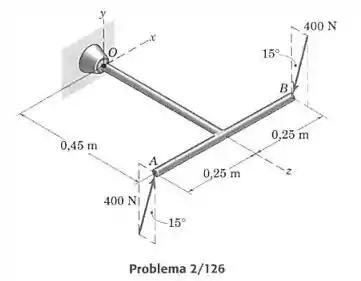
Passo 1
Vamos calcular o momento em torno de por uma análise escalar, pois é fácil encontrarmos as componentes das forças e as distâncias até o ponto . Calculamos primeiro as componentes das forças nas direções e (as forças não tem componente ) e então multiplicamos os módulos pelos braços de alavanca. O sinal dos momentos será dado pela regra da mão direita.
Passo 2
Primeiro vamos decompor as duas forças. Vamos chama-las de e . Os ângulos entre as forças e a vertical são de 15°, então as componentes de são:
Não vamos nos preocupar com sinal agora, pois o sinal dos momentos será determinado pela regra da mão direita. As componentes de são iguais em módulo:
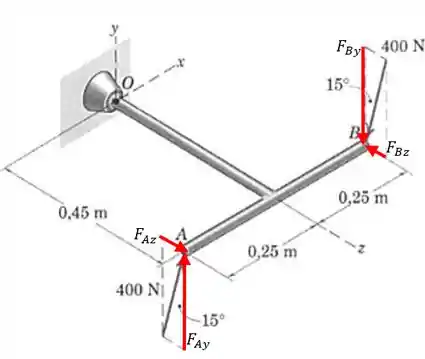
Passo 3
Agora vamos calcular o momento para cada uma das três direções: , e . Primeiro para a direção . As forças e têm linha de força passando pelo eixo , então não causam momento. As forças e têm mesmo módulo e mesma distância até o eixo de 0,45 m, e fazem momentos em sentidos contrários em torno de . Logo os dois momentos se anulam:
Calculamos então o momento para o eixo . As forças e são paralelas ao eixo, então não causam momento. As forças e têm mesmo módulo 103,4 N e mesma distância até o eixo , igual a 0,25 m. Além disso, as duas causam momento no mesmo sentido. Pela regra da mão direita, vemos que esse sentido é o positivo no eixo , pois quando fechamos os dedos no sentido de giro das forças nosso polegar aponta para cima. Então o momento total no eixo causado pelas duas forças é:
Agora para o eixo . As forças e são paralelas ao eixo, então não causam momento. As forças e têm mesmo módulo 346,4 N e mesma distância até o eixo , igual a 0,25 m. Além disso, as duas causam momento no mesmo sentido. Pela regra da mão direita, vemos que esse sentido é o negativo no eixo , pois quando fechamos os dedos no sentido de giro das forças nosso polegar aponta para o sentido contrário de . Então o momento total no eixo causado pelas duas forças é:
Multiplicando as componentes pelos vetores unitários , e , obtemos o vetor :