Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 46

Determine o momento combinado em relação ao ponto O devido ao peso da caixa de correio e a travessa A B . A caixa de correio pesa 4   l b e o membro transversal uniforme pesa 10   l b . Ambos os pesos atuam na geometria centros dos respectivos itens.

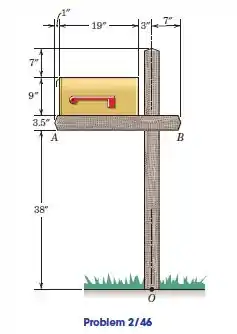
Passo 1

Olá, tudo joinha? Esse problema é bem simples, rapidão a gente faz!

Vamos começar desenhando, colocando o peso de 4   l b no centro de massa da caixa de correios, e o peso de 10   l b no centro de massa do membro transversal.

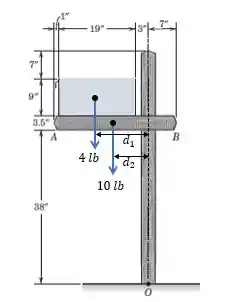
Precisamos determinar o momento combinado em relação ao ponto O dos pesos de 4   l b e de 10   l b . Para isso precisamos encontrar as distâncias d 1 e d 2 .

O comprimento da caixa de correios é 19   i n , então

d 1 = 19   i n 2 + 3   i n

d 1 = 12,5   i n

E o comprimento do membro transversal é

1   i n + 19   i n + 3   i n + 7   i n = 30   i n

Então, a distância horizontal do centro de massa até ponto O será

d 2 = 30   i n 2 - 7   i n

d 2 = 8   i n

Passo 2

Temos as distâncias, agora podemos calcular o momento.

Considerando o sentido anti-horário como positivo:

M O = F 1 d 1 + F 2 d 2

M O = 4   12,5 + 10   8

M O = 130   l b ⋅ i n

no sentido anti-horário.

Resposta

M O = 130   l b ⋅ i n   ( n o   s e n t i d o   a n t i - h o r á r i o )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os componentes escalares R a e R b da força R ao longo dos eixos não retangulares a e b . Determine também a projeção ortogonal P a de R sobre o eixo a .
A razão entre a força de sustentação L e a força de arraste D , para um aerofólio simples, é L / D = 10 . Se a força de sustentação em uma seção curta do aerofólio vale 200N , calcule o módulo da forç
Deseja-se remover o pino da madeira pela aplicação de uma força ao longo de seu eixo horizontal. Um obstáculo A impede um acesso direto, de modo que duas forças, uma de 1,6k N e a outra P , são aplica
Em que ângulo θ uma força de 800N deve ser aplicada para que a resultante R das duas forças tenha um módulo de 2000N ? Para esta condição, determine o ângulo β entre R e a vertical.
Os cabos de sustentação A B e A C estão presos no topo da torre de transmissão. A força trativa no cabo A C vale 8k N . Determine a força trativa T necessária no cabo A B , tal que o efeito resultante