Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 77
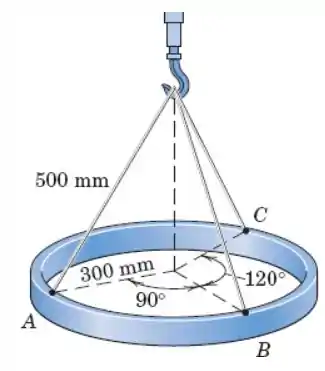
Um anel uniforme de aço, com de diâmetro, tem uma massa de e está sustentado por três cabos, cada um com de comprimento, presos aos pontos , como mostrado. Calcule a força trativa em cada cabo.
Passo 1
Como os cabos não estão distribuídos pelo anel de forma simétrica, não podemos garantir que as forças são iguais em todos eles. Vamos ter que escrever as forças em forma vetorial. Para isso, vamos encontrar vetores unitários na direção de cada cabo
Pelo teorema de pitágoras, podemos calcular que a distância vertical entre o gancho e o centro do anel é (porque temos um triângulo ), então:
Reorganizando um pouco ficamos com os seguintes vetores unitários:
E para a força peso temos
Passo 2
Para encontrar a força vetorial de cada uma das forças só precisamos multiplicar o módulo da força pelo vetor unitário correspondente. Agora vamos aplicar uma equação de equilíbrio: a força resultante sobre o anel tem que ser nula
E como cada componente tem que se anular, vamos com um sistema de três equações e três variáveis
Então só precisamos resolver esse sistema.
Passo 3
Primeiro vamos multiplicar as duas últimas equações por 5 e a primeira por 10, de modo a obter
Da primeira e da segunda equação tiramos as seguintes conclusões
E substituindo isso na terceira equação
Agora, substituindo esse resultado nas duas expressões de antes
Pronto, tá resolvido nosso exercício.
Resposta
As forças no cabo são