Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.3 - Ex. 27
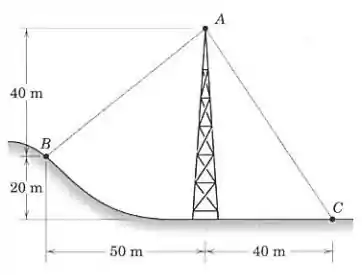
Os cabos de sustentação e estão presos no topo da torre de transmissão. A força trativa no cabo vale . Determine a força trativa necessária no cabo , tal que o efeito resultante das duas forças trativas nos cabos seja uma força direcionada para baixo no ponto . Determine o módulo desta força.
Passo 1
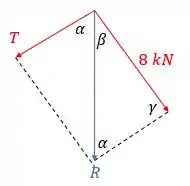
Todas as forças, incluindo a resultante, foram representadas na figura a seguir:
Podemos determinar todos os ângulos com base nas dimensões indicadas na figura do enunciado:
Passo 2
Show! Agora utilizamos a lei dos senos para calcular a tração :
Passo 3
Podemos usar de novo a lei dos senos, desta vez para determinar :
Resposta
Exercícios de Livros Relacionados
O cabo A C exerce sobre a viga A B a força P dirigida ao longo da linha A C . Sabendo que P tem uma componente vertical de 1560N , determine (a) a intensidade da força P , (b) sua componente horizonta
Determine os componentes x e y de cada uma das forças indicadas.
O cabo de sustentação B D exerce no poste telefônico A C uma força P dirigida ao longo de B D . Sabendo que P tem uma componente de 180N perpendicular ao poste A C , determine (a) a intensidade da for
Determine os componentes x e y de cada uma das forças indicadas.
Sabendo que α = 40 ° , determine a resultante das três forças indicadas.