Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 48
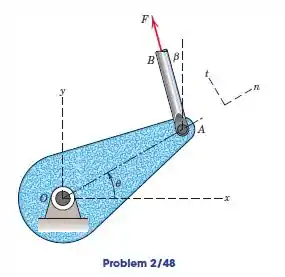
A manivela do Prob. 2/10 é repetido aqui. Se , e , determine o momento da força de magnitude em relação ao ponto .
Passo 1
Olá, tudo bem com você?
Nesse problema temos que determinar o momento da força em relação ao ponto . O enunciado nos informa que , e . Vamos começar ilustrando:
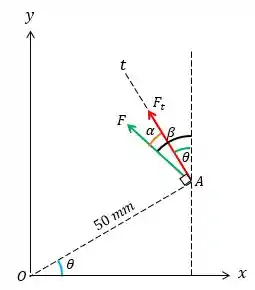
Precisamos encontrar o ângulo , para determinar a componente .
Sabendo que e :
Prontinho, já temos o valor de , então,
Passo 2
Agora vamos calcular o momento!
Considerando o sentido anti-horário como positivo:
no sentido anti-horário.
*Veja que antes de calcular, convertemos o comprimento do segmento de para .
Resposta
Exercícios de Livros Relacionados
Se a intensidade da força resultante que atua sobre o suporte deve ser 450N direcionada ao longo do eixo u positivo, determine a intensidade de F 1 e sua direção ϕ .
Especifique a intensidade de F 3 e seus ângulos de direção coordenados α 3 , β 3 , γ 3 de modo que a força resultante seja F R = { 9 j } kN.
2.6. Se a força F precisa ter uma componente ao longo do eixo u com F u = 6k N , determine a intensidade de F e de sua componente F v ao longo do eixo v.
2.3. A força F = 900N atua sobre a estrutura. Decomponha essa força nas componentes que atuam ao longo dos membros AB e AC, e determine a intensidade de cada componente.
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.