Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 17
Determine o momento da força F = {50i - 40j + 20k} kN em relação ao eixo AB. Expresse o resultado
como um vetor cartesiano.
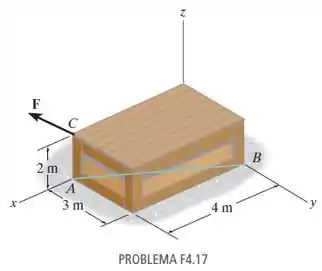
Fonte: Estática Mecânica para Engenharia – 14ª ed
Passo 1
E aí galera top!!
Estamos começando a pegar o jeito hein!!
A segunda coisa é que nunca devemos esquecer que o momento de uma força é sempre o produto da força pela distância horizontal que esta está aplicada do ponto de referência. E detalhe: o ângulo entre essa força e a linha horizontal é sempre .
O segundo ponto é que nesse tipo de problema, em que é pedido o momento de uma força em relação a um segmento de reta, ou a uma barra, podemos encontrar assim:
Passo 2
Em que o pode ser encontrado da seguinte forma:
Pronto, agora o vetor posição da Força em relação à AB pode ser tanto o ponto C (onde encontra-se a Força) em relação tanto ao ponto B quanto ao ponto A. Faremos aqui em relação ao ponto B:
E a força F já foi dada como vetor cartesiano, para a nossa alegria kkk.
Passo 3
Assim, o Momento da força F em relação à AB, fica:
Assim, aplicando o determinante, temos:
E como , podemos transformar em vetor:
Resposta
Portanto: