Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 8

F4.8. Determine i momento resultante produzido pelas forças em relação ao ponto O.

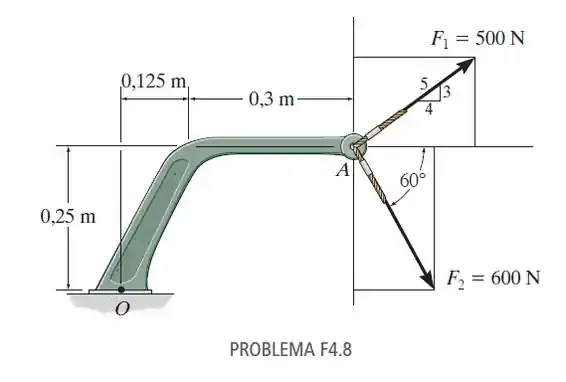
Passo 1

Falaaaa... belezita??

Caramba... calcular o momento desse negócio todo parece que vai dar trabalho, heim...

Mas nem vai. Cola comigo que matamos rapidinho.

Como o momento é:

M = F d

A gente pode dividir em duas partes. Vamos decompor as forças em x e y, e depois calculamos o momento de x e y separadamente.

Passo 2

Em x, as forças ficam:

F 1 x = 500 cos ⁡ θ

F 1 x = 500   4 5

F 1 x = 400   N

F 2 x = 600 cos ⁡ 60 °

F 2 x = 600 1 2

F 2 x = 300   N

E repara que a distância de y é 0,25m, então: (considerando o sentido anti-horário positivo)

M O y = - 400 0,25 - 300 0,25

M O y = - 100 - 75

M O y = - 175   N ⋅ m

Em y, as forças ficam:

F 1 y = 500 sen ⁡ θ

F 1 y = 500   3 5

F 1 y = 300   N

F 2 y = 4 = 6 00 sen ⁡ 60 °

F 2 y = 6 00 3 2

F 2 y = 520   N

E a distância de x é 0,125+0,3 = 0,425m, então:

M O x = 300 0,425 - 346,41 0,425

M O x = 12 8 - 221

M O x = - 93   N ⋅ m

Agora é só somar os dois:

M O = - 175 - 93

M O = - 269   N ⋅ m

Ufa... Essa foi, heim. Bora pra mais uma??

Resposta

M O = - 269   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os dois garotos empurram o portão com forças de F B = 250N e F A = 150N como mostrado. Determine o momento de cada força em relação a C . Em que sentido o portão girará, horário ou anti-horário? Despr
Determine a direção θ ( 0 ° ≤ θ ≤ 180 ° ) da força F de modo que ela produza o momento máximo em relação ao ponto A . Calcule esse momento.
As pinças são usadas para prender as extremidades do tubo de perfuração P . Determine o torque (momento) M P que a força apliada F = 750N exerce sobre o tubo em relação ao ponto P como uma função de θ
Sérios danos ao pescoço podem ocorrer quando um jogador de futebol americano é atingido na proteção de rosto de seu capacete da maneira mostrada, causando um mecanismo de guilhotina. Determine o momen
Determine o momento da força F em relação ao ponto A como uma função de θ . Represente os resultados de M (ordenada) em função de θ (abscissa) para ( 0 ° ≤ θ ≤ 180 ° ) .