Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 11
Determine o momento da força F em relação ao ponto O. Expresse o resultado como um vetor cartesiano.
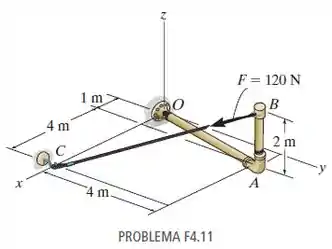
Fonte: Estática Mecânica para Engenharia – 14ª ed
Passo 1
Tudo bem com vocês coisas lindas?!
Espero que sim haha!
Bem, a partir daqui, já começamos a perceber que podemos encontrar o valor do momento em forma cartesiana, e que é tão legal quanto a forma escalar.
Lembrando sempre que: o diagrama do corpo livre é essencial para o entendimento e para a resolução das questões.
A segunda coisa é que nunca devemos esquecer que o momento de uma força é sempre o produto da força pela distância horizontal que esta está aplicada do ponto de referência. E detalhe: o ângulo entre essa força e a linha horizontal é sempre .
Passo 2
Aqui, vamos mostrar que a forma vetorial pode ser encontrada sem a necessidade do diagrama de corpo livre:
O Momento de uma força é dado lá no capítulo, mais precisamente eq. 4.7, por:
Nesse caso, precisamos encontrar o , que é a posição da força.
Então:
Passo 3
O próximo passo é encontrar o vetor F, assim:
E por fim, aplicar o produto vetorial do braço em relação ao ponto O.
Aqui, podemos escolher usar a posição ou , pois ambos os braços estão em contato com o ponto O e têm a força F passando em seu domínio.
Vamos escolher a posição :
Assim, aplicando o determinante, temos:
Então
Resposta
Portanto: