Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 1

Determine o momento de inércia da área sombreada em relação ao eixo  x .

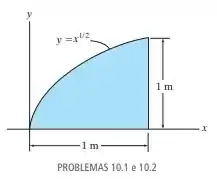
Passo 1

Falaiii galerinha, show de bola??

Vamos começar desenhando o diagrama de corpo livre do elemento diferencial da área sombreada.

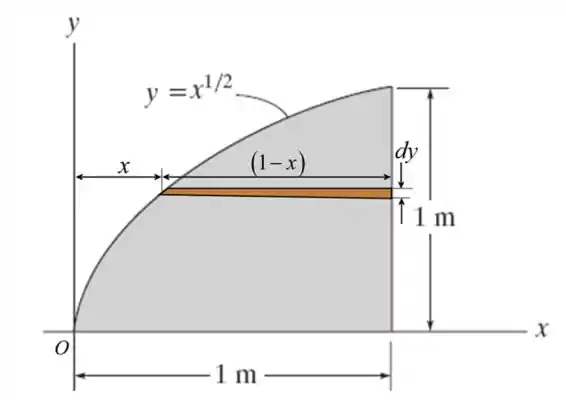
Passo 2

Calcule a área do elemento diferencial

d A = 1 - x d y                         ( 1 )

Considere a equação da curva e escreva a relação em termos de x

y = x 1 2

x = y 2

Substituindo y 2 por x na expressão (1)

d A = 1 - x d y

d A = 1 - y 2 d y

Passo 3

Calcule o momento de inércia dos sombreados em torno do eixo x.

I x ∫ A y 2 d A

I x = ∫ 0 1 y 2 1 - y 2 d y

I x = ∫ 0 1 ( y 2 - y 4 ) d y

I x = y 3 3 0 1 - y 5 5 0 1

I x = 1 3 - 1 5

I x = 0.133   m 4

Portanto, o momento de inércia do sombreado é sobre o eixo x é 0.133   m 4

Resposta

I x = 0.133   m 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma batuta consiste em um fino cilindro metálico de massa M e comprimento L. Cada extremidade possui uma tampa de borracha de massa m, e cada tampa pode ser tratada com precisão como uma partícula nes
Um volante de motor a gasolina deve fornecer uma energia cinética igual a 500J, quando sua velocidade angular diminui de 650 rev/min para 520 rev/min. Qual é o momento de inércia necessário?
Calcule o momento de inércia em relação a cada um dos seguinte eixos para um eixo de 0.300 cm de diâmetro, 1.50 m de comprimento e massa igual a 0.0420kg. Use as fórmulas da Tabela 9.2.Em relação a um
Pequenos blocos, todos com a mesma massa m, estão presos às extremidades e ao centro de uma barra de comprimento igual a L. Calcule o momento de inércia do sistema em relação a um eixo perpendicular à
Fator de escala de I.Quando multiplicamos todas as dimensões de um objeto por um fator de escala f, sua massa e seu volume ficam multiplicados por f^3O momento de inércia ficará multiplicado por qual