Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 12

Determine o momento de inércia da área sombreada em relação ao eixo y .

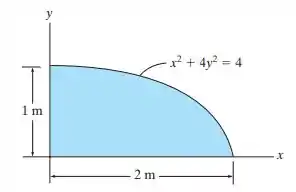
Passo 1

Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.

Este problema nos pede para determinarmos o momento de inercia em relação ao eixo y da figura. Sabemos que ele é dado por:

I y = ∫ x 2   d A

Primeiro, temos que determinar o elemento diferencial, neste caso, ele vai ser paralelo ao eixo y , logo:

d A = y   d x

Em seguida, vamos isolar y na equação que determina a área, temos:

x 2 + 4 y 2 = 4 y = 1 2 4 - x 2

Então, devemos substituir esta equação na relação do elemento diferencial. Fica assim:

d A = y   d x d A = 1 2 4 - x 2   d x

Passo 2

Agora que já determinamos o elemento diferencial, vamos substituir estes termos na relação para o momento de inércia no eixo y , temos:

I y = ∫ x 2   d A I y = ∫ 0 2 x 2 1 2 4 - x 2   d x  

Integrando:

I y = 1 2 - x 4 4 - x 2 3 + 1 2 x 4 - x 2 + 4 x 2   0 2 I y = π 2   m 4

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

I y = π 2   m 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de inércia da área sombreada em relação ao eixo  y .
Determine o momento de inércia da área sombreada em relação ao eixo y .
Determine o momento de inércia da área sombreada em relação ao eixo  y .
Determine o momento de inércia da área sombreada em relação ao eixo  y .
Determine o momento de inércia da área sombreada em relação ao eixo  y .