Enunciado
Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 99
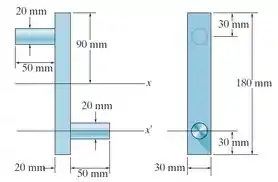
Determine o momento de inércia de massa da manivela em relação ao eixo . O material é aço, com densidade .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos calcular o momento de inércia de massa de um sistema, composto por uma barra e duas manivelas, em relação ao eixo .
Vamos começar relembrando da fórmula do momento de inércia de massa de cada um dos componentes em relação ao eixo que passa pelo centro de massa (paralelo ao eixo ). Para a barra, temos:
Sendo a sua massa, e . Já para a manivela, temos:
Sendo .
Bom, já deu para perceber que temos um problema em relação as fórmulas não serem em relação ao eixo , mas sim do eixo que passa pelo centro de massa. Por causa disto, vamos ter que trabalha com o teorema de eixos paralelos.
Só que nós só veremos este teorema depois, pois temos um problema maior antes: qual é a massa dos componentes??? Então, vamos calculá-los!
Passo 2
Vamos calcular a massa da barra e da manivela. Aqui é jogo fácil. Basta lembrar que a massa é o produto da densidade pelo volume! Portanto, começando pela barra, temos:
Já para a manivela, temos:
E assim terminamos de determinar a massa dos componentes!
Passo 3
Para que a gente consiga calcular o momento de inércia, vamos nos lembrar do teorema dos eixos paralelos. Ele nos diz que:
Sendo o momento de inércia que passa pelo centro de massa da peça, o momento de inércia que queremos e a distância entre os dois eixos.
Para o caso da questão, o centro de massa da barra coincide com o eixo . Logo, para a barra temos . Já para a manivela os dois eixos não coincidem. Ambos distam . Portanto, temos:
E assim finalizamos a questão!