Enunciado
Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 109
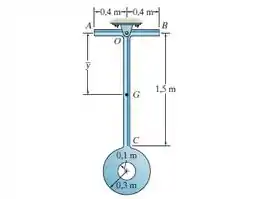
O pêndulo consiste em duas hastes finas e , que tem massa de . A placa fina tem massa de . Determine a localização do centro de massa do pêndulo; depois, determine o momento de inércia de massa do pêndulo em relação a um eixo perpendicular à página e que passa por .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão bem grande, que vamos ter que realizar vários passos para poder resolvê-la.
De início, a questão nos pede para calcular o centroide do pêndulo e depois o momento de inércia de massa do pêndulo em relação ao eixo que passa pelo centroide. Sendo assim, vamos começar determinando o centro de massa do pêndulo
Então, vamos utilizar o bom e velho método de dividir para conquistar. Vamos dividir a nossa figura em quatro seções, sendo elas: haste , haste , disco de raio e disco de raio .
Percebam que este último disco é a parte vazada da placa fina. Portanto, quando formos fazer os cálculos do momento de inércia e centro de massa, não esqueçam de colocar o sinal dele negativo!!!
Agora, vamos as contas!
Passo 2
Novamente, vamos começar calculando o centro de massa do nosso pêndulo,
Então, para nos auxiliar nas contas, vamos montar uma tabela com os valores do centroide e os respectivos produtos pela área (e embaixo o somatório).
Vejamos só abaixo:
Portanto, o centro de massa estará na posição:
E assim finalizamos a primeira parte da questão!
Passo 3
Agora nós temos que descobrir o momento de inércia do pêndulo em relação a um eixo perpendicular que passa por .
Para isto, temos que fazer um procedimento semelhante ao do Passo anterior, só que para o momento de inércia.
Além disto, temos uma preocupação. O momento de inércia que nós calculamos é em relação ao centroide da seção, e não em relação ao eixo . Por causa disto, temos que utilizar o teorema dos eixos paralelos, que nos diz que:
Sendo o momento de inércia que passa pelo centro de massa da peça, o momento de inércia que queremos e a distância entre os dois eixos.
Relembrando também, a fórmula para momento de inércia passando pelo centro da figura é:
Para a haste, a massa é . Já para o disco, a massa é .
Compilando todos os dados em uma tabela, temos:
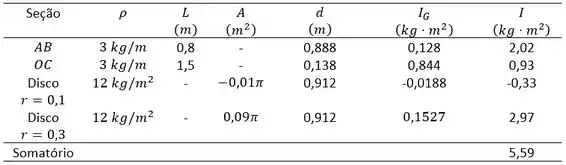
Então o momento de inércia será:
E assim finalizamos a questão!