Enunciado
Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 108
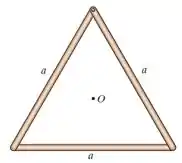
Cada um dos três elementos finos tem massa . Determine o momento de inércia do conjunto em relação a um eixo perpendicular à página e que passa pelo ponto central .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos calcular o momento de inércia de massa do conjunto em relação ao eixo que passa por , que é o centro de massa do triângulo equilátero.
Por definição, o momento de inércia de uma haste em relação ao eixo perpendicular ao plano e que passa pelo seu centro de massa é dado por:
Só que nós queremos em relação ao ponto . Por causa disto, precisamos utilizar o teorema dos eixos paralelos, que nos diz que:
Sendo o momento de inércia que passa pelo centro de massa da peça, o momento de inércia que queremos e a distância entre os dois eixos.
Calculado o valor para cada uma das barras, basta somarmos o valor que assim teremos o momento de inércia do sistema.
Passo 2
Então, precisamos começar identificando a distância das hastes até o ponto . Por definição, as distâncias das hastes ao ponto são iguais entre si e expressas por:
Então, o momento de inércia de uma haste em relação ao ponto é:
E por fim, como temos 3 hastes, o momento de inércia do sistema será:
E assim finalizamos a questão!