Enunciado
Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 104
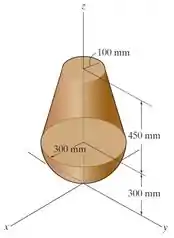
Determine o momento de inércia de massa do conjunto em relação ao eixo . A densidade do material é .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos calcular o momento de do conjunto todo, que é composto por um tronco de cone e por um hemisfério (metade de uma esfera).
Para o hemisfério, o momento de inércia é:
Agora, para o tronco de cone, temos um problema. Nós não temos nenhuma relação para esta figura. A única relação que temos é para um cone inteiro, que é dado por:
E agora???
Bom, o que temos que fazer é calcular o momento de inércia para um cone completo (que engloba o tronco de cone) e depois subtrair o momento das partes que estão faltando (o topo do cone e a depressão)
Então, vamos começar identificando as dimensões do cone inteiro e do pedaço que iremos retirar dele (e que assim resulta no tronco de cone).
Passo 2
Vamos começar pelo cone maior. Ele tem raio de base igual a . Já a altura a gente não conhece (pois temos apenas a altura do tronco de cone).
Mas não é nada impossível de conseguirmos esta dimensão. Por relação de triângulo, temos:
Já a parte do topo do cone que está faltando terá raio e altura .
E assim a gente encontrou as dimensões de cada cone.
Passo 3
Como na fórmula do momento de inércia nós precisamos da massa de cada um dos componentes, vamos calculá-los agora.
Aqui é jogo fácil. Basta lembrar que a massa é o produto da densidade pelo volume! Portanto, começando pelo cone maior, temos:
Já para o topo do cone que está faltando, temos:
Por fim, a massa do hemisfério será:
E assim terminamos de determinar a massa dos componentes!
Passo 4
Para finalizarmos a questão, basta calcularmos o momento de inércia do cone completo e subtrair dos pedaços que faltam. Sendo assim, temos:
E assim finalizamos a questão!