Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 93
Determine o momento em termos da carga e da dimensão a de modo que a deflexão no centro da viga seja nula. é constante.
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat. Aqui vamos usar o método da superposição. Nele, vamos usar algumas situações estáticas distintas, que quando sobrepostas, dão a nosssa viga fofa do enunciado.
Queremos o valor de para que a defexão no meio dessa viga se anule. Como a gente quer uma informação no meio da viga, podemos começar substituindo nossa viga do enunciado por uma mais simples e estaticamente equivalente. Essa por exemplo:
Percebe que para aquele intervalo no meio da viga, de onde a gente queria as informações, nada mudou. Por que? Porque não faz diferença estaticamente para esse vão se a gente mover os momentos para os apoios.
Como não fizemos nenhuma mudança nesse intervalo do meio (no vão), não causamos nenhuma mudança nas deflexões nesse intervalo. (obviamente causamos mudança nos intervalos da viga em balanço, mas eles não são importantes agora para gente).
E para chegar nessa viga repaginada, podemos pensar na sobreposição dessas situações:
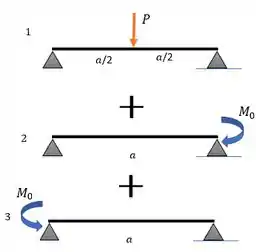
A ideia aqui é que a gente pode separar a situação da nossa viga em situações que já são tabeladas. E depois podemos só somar os resutados. Aí evita mais continhas. Bora ver como isso fica!
Passo 2
Lembrando que o comprimento da nossa viga é .
Para esta viga, no caso 1, temos uma fórmula tabelada para a deflexão no meio da viga. Cê acha no apêndice C.
Para o caso 2, fazemos a mesma coisa. Só cuidado com a orientação do momento que lá no apêndice está oposta a nossa. Então a gente multiplica noss por
(obs: no apêncide o denominador dessa fórmula está diferente, mas eles são numericamente parecidos. Você pode usar aquela fórmula ou essa. Vou usar essa para a gente chegar no gabarito)
Percebe que o caso 3 é o mesmo do anterior, mas espelhado. Isso quer dizer que a deflexão no meio da viga deles é igual:
Passo 3
Pelo princípio da superposição, a deflexão resultante no meio da nossa viga em questão deve ser a soma das deflexões de cada caso que a gente calculou:
Mas o enunciado pediu o valor de que zera essa deflexão. Então a gente faz .