Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 2ii

Determine os momentos das forças representadas na próxima figura, em relação às origens dos sistemas cartesianos indicados

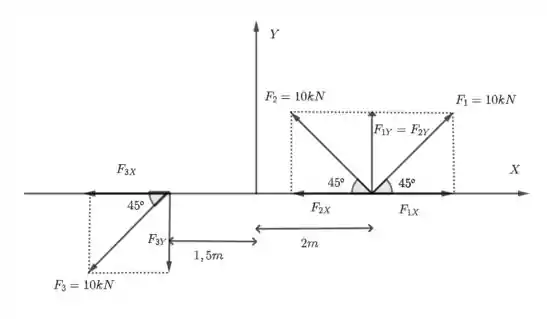
Passo 1

A sacada dessa questão é lembrar que o momento resultante é igual a soma vetorial dos momentos de cada força, ou seja, M → = M → 1 + M → 2 + M → 3 . Então podemos calcular o momento de cada força separadamente. Bem mais fácil né?

A primeira força tem módulo 10   k N faz um ângulo de 45   ° em relação a x , e não tem componente na direção z . Então,

F 1 X   = F 1 c o s   θ   = 10   k N c o s 45   ° = 1 0   k N ⋅ 0,707 = 7,07   k N    

F 1 Y   = F 1   s e n     θ = 10   k N   s e n   45   ° = 10   k N ⋅ 0,707 = 7,07   k N

F Z = 0

A origem dessa força é o ponto ( 2,0 , 0 ) . Agora é só substituir na fórmula:

M 1 X = 0 - 0 ⋅   7,07   k N = 0

M 1 Y = 0 ⋅ 7,07 - 0 = 0

M 1 Z = 2 m ⋅   7,07 - 0 ⋅ 7,07   k N = 14,14   k N m

Ou seja, M 1 → =   14,14   (   k N m )   k ^ .

Passo 2

A segunda força também tem módulo 10   k N e origem ( 2,0 , 0 ) , mas o ângulo não será 45   ° . Na verdade, temos que tomar o ângulo em relação a direção positiva de x , contando no sentido anti-horário. Nesse caso, temos 180   ° - 45   ° = 135   ° . Agora ficou fácil calcular as componentes da segunda força

F 2 X   = F 2 c o s   θ   = 10   k N c o s 135   ° = - 10   k N ⋅ 0,707 =   - 7,07   k N    

F 2 Y   = F 2   s e n     θ = 10   k N   s e n   135   ° = 10   k N ⋅ 0,707 = 7,07   k N

F 2 Z = 0

Percebeu que a componente F 2 x ficou com sinal contrário? Agora vamos obter o momento dessa força

M 2 X = 0 - 0 ⋅   7,07   k N = 0

M 2 Y = 0 ⋅ ( - 7,07 ) - 0 = 0

M 2 Z = 2 m ⋅   7,07 - 0 ⋅ ( - 7,07   k N ) = 14,14   k N m

⇒ M 2 → = 14,14   (   k N m )   k ^ .

Passo 3

A terceira força também tem módulo 10   k N mas origem ( 1,5 ,   0 ,   0 ) , e o ângulo também não será 45   ° . O ângulo na verdade será 180 ° + 45 ° = 225 ° . Agora é só seguir o mesmo processo para obter as componentes da força

F 3 X   = F 3 c o s   θ   = 10   k N c o s 225   ° = - 10   k N ⋅ 0,707     = 7,07   k N

F 3 Y   = F 3   s e n     θ = 10   k N   s e n   225   ° = - 10   k N ⋅ 0,707   = 7,07   k N

F 3 Z = 0

e o momento da força

M 3 X = 0 - 0 ⋅ ( -   7,07   k N ) = 0

M 3 Y = 0 ⋅ ( - 7,07 ) - 0 = 0

M 3 Z = 1,5 m ⋅ ( -   7,07 ) - 0 ⋅ ( - 7,07   k N ) = - 10,605   k N m ≈ - 10,61   k N m

⇒ M 3 → = - 10,61   ( k N m )   k ^ .

Assim, o momento resultante é

M → = M → 1 + M → 2 + M → 3 = ( 14,14   k N m + 14,14   k N m - 10,61   k N m ) k ^ = 17,67   (   k N m ) k ^

Resposta

M 1 → = 14,14   (   k N m )   k ^

M 2 → = 14,14   (   k N m )   k ^

M 3 → = - 10,61   ( k N m )   k ^

M → = 17,67   (   k N m ) k ^

Exercícios de Livros Relacionados

F4.8. Determine i momento resultante produzido pelas forças em relação ao ponto O.
Determine o momento resultante produzido pelas forças em relação ao ponto O.Fonte: Estática Mecânica para Engenharia – 14ª ed
Determine o momento da força em relação ao ponto O .
A grua torre é usada para içar a carga de 2 Mg para cima em velocidade constante. A lança BD de 1,5 Mg, a lança BC de 0,5 Mg e o contrapeso C de 6 Mg possuem centros de massa em G1, G2 e G3, respectiv
A grua torre é usada para içar a carga de 2 Mg para cima em velocidade constante. A lança BD de 1,5 Mg, a lança BC de 0,5 Mg e o contrapeso C de 6 Mg possuem centros de massa em G1, G2 e G3, respectiv