Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 54
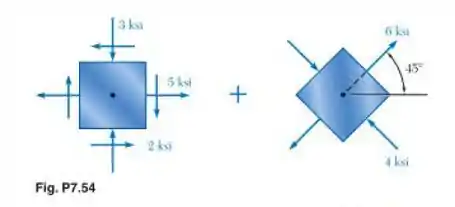
Determine os planos e tensões principais para o estado plano de tensão resultante da superposição dos dois estados de tensão mostrados.
Passo 1
Eaeee pessoal, beleza? Bora pra mais um exercício? Então tá, para determinar os planos e tensões principais para o estado plano de tensão resultante dos dois estados, precisamos primeiro expressar o estado de tensões da direita em termos de suas componentes horizontais e verticais, e para fazer isso, vamos contar com o auxílio do círculo de Mohr, rotacionando o elemente de 45°, ou seja, percorrendo 90° no círculo, para encontrar o estado desejado.
Depois disso é só somar as componentes dos dois estados para obter o estado resultante e aí desenhar o círculo de Mohr para esse estado para poder encontrar os planos e as tensões principais do estado resultante. Então vamos lá!
Passo 2
Vamos começar desenhando o círculo de Mohr para o estado da direita, onde teremos:
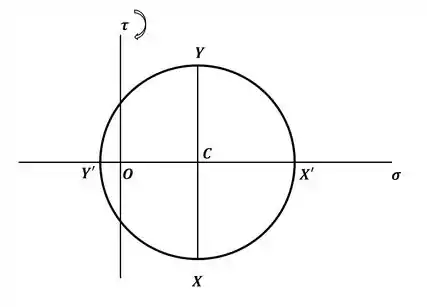
Como o estado da direita dado é um estado de tensão puro, ficou fácil encontrar os pontos X’ e Y’ desse estado, e podemos calcular o raio desse círculo pela diferença entre as duas tensões, onde teremos:
Substituindo os valores conhecidos, chegamos em:
Dessa forma, ao rotacionar o elemento diferencial de 45° no sentido horário, ou seja, 90° no círculo de Mohr, os novos pontos serão X e Y já desenhados no círculo acima. A tensão de cisalhamento para esses pontos será o próprio raio do círculo, ou seja:
Agora, a coordenada para a tensão, que é a mesma para os dois pontos, ou seja, teremos , pode ser encontrada pela diferença:
Passo 3
Beleza! Agora, com as tensões normais e de cisalhamento encontradas no passo 2, podemos desenhar o seguinte estado de tensão:
Então, somando as componentes desse elemento com as componentes do elemento da esquerda fornecido no enunciado, chegamos no seguinte elemento resultante:
E, para esse elemento diferencial, teremos o seguinte círculo de Mohr:
Passo 4
Beleza, estamos quase lá! Agora, para encontrar a direção dos planos principais, basta encontrar o valor de mostrado no círculo de Mohr do passo 3, então, por trigonometria, teremos:
Então, para encontrar o valor de , precisamos encontrar antes a tensão média, pois os outros dois valores da equação nós já temos lá do elemento de tensão. Então, sabendo que a tensão média é dada por:
Então, substituindo os valores conhecidos na equação para , chegamos em:
Então, sabendo que essa é uma direção principal, e a outra fica a uma rotação de 90° do elemento diferencial (e 180° no círculo de Mohr), a outra direção principal será:
Estamos quase lá, faltam só as tensões principais agora.
Passo 5
Agora para encontrar as tensões principais ficou fácil, já que elas são dadas por:
Nós já temos o valor de , que vimos ali em cima e o valor do raio do círculo precisamos calcular. Então, tomando como base o círculo de Mohr esboçado no passo 3, temos a seguinte relação para o raio:
Substituindo os valores conhecidos, teremos:
Agora sim podemos calcular as tensões principais, que serão então:
Prooonto! Fechamos mais um exercício. Valeeu!