Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 59
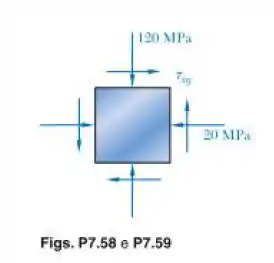
Para o elemento mostrado, determine o intervalo de valores de para os quais a tensão de cisalhamento máxima no plano da tensão é igual ou menor que 150 MPa.
Passo 1
Fala pessoal, tudo bem? Vamos riscar mais um exercício da sua lista? Para resolver esse exercício, vamos utilizar a equação do raio do círculo de Mohr, dada por:
Mas por que? Porque ela tem a tensão de cisalhamento que estamos interessados em descobrir. Agora, o enunciado nos falou para limitar a tensão de cisalhamento máxima no plano da tensão em 150 MPa, e, nós sabemos que no estado plano da tensão a tensão de cisalhamento máxima é o próprio raio do círculo. Então esse ficou fácil né?! Vamos lá!
Passo 2
Vamos começar escrevendo nossas componentes de tensão que vem do elemento dado no enunciado, onde temos:
Então, como sabemos que no estado plano da tensão a tensão de cisalhamento máxima é o próprio raio do círculo, teremos:
Passo 3
Agora temos todos os valores para usar a nossa equação do raio do círculo de Mohr, onde temos:
Então, isolando a tensão de cisalhamento dessa equação, temos:
Substituindo os valores conhecidos nessa equação, chegamos em:
Opa! Então isso quer dizer que o intervalo de valores aceitáveis para será:
É isso aí! Acabamos mais um!