Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 152
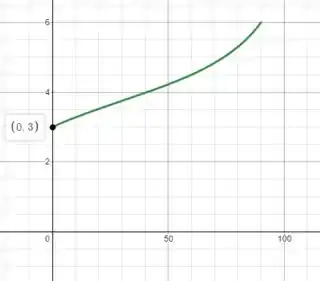
Determine e plote as forças em todos os membros da treliça simples carregada como funções do ângulo ao longo do intervalo . Indique os valores mínimos para as forças nas barras AC e CD e os valores nos quais esses mínimos ocorrem.
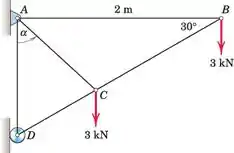
Passo 1
Primeiro, podemos analisar a junta B para determinar as forças nos membros AB e BC
Observe que as forças nos membros AB e BC são constantes para qualquer valor de a, uma vez que a mudança do ângulo a não os afeta.
Observe também que assumiremos que todos os membros desconhecidos estão em tensão
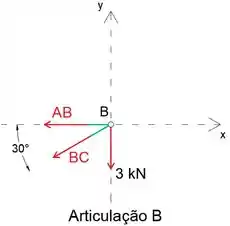
Aplicando as equações de equilíbrio, determinaremos as forças nos membros AB e BC
Passo 2
Como obtivemos o resultado negativo, isso significa que o membro está em compressão
Substitua BC por seu valor
Agora podemos analisar a junta C.
Passo 3
Observe que criamos um sistema de coordenadas mOn, onde o eixo m é paralelo ao membro BCD, a fim de facilitar os cálculos.
Observe também que assumimos que todos os membros desconhecidos estão sob tensão, portanto, os membros estarão em compressão quando seu valor for negativo.
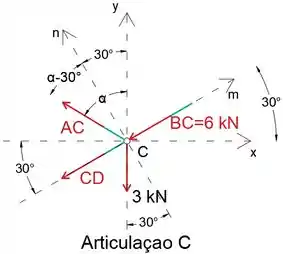
Ao igualar a soma das forças na direção n a zero, podemos determinar a força AC
Passo 4
Podemos ver que o membro está em tensão (valor positivo) e a força de tensão mínima do membro AC é:
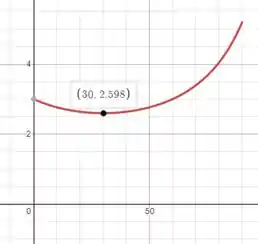
Ao igualar a soma das forças na direção x a zero, podemos determinar a força CD
Substitua AC pela expressão (1)
Podemos ver que o membro está em compressão (valor negativo) e a força de compressão mínima do membro CD é:
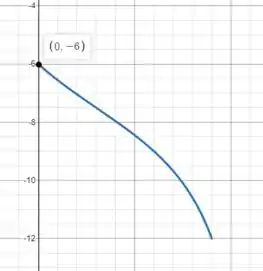
Finalmente, podemos analisar a junta D
Equacionando a soma das forças na direção y a zero, podemos determinar a força AD
Substitua CD pela expressão (2)
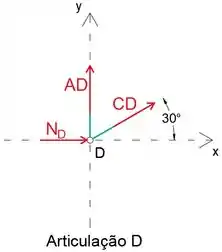
Passo 5
Podemos ver que a barra está em tensão (valor positivo) e a força de tensão mínima da barra AD é:
