Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 115
Calcule os componentes x e y de todas as forças que atuam em cada membro do quadro carregado.
Passo 1
Primeiro, vamos desenhar o diagrama de corpo livre de todo o sistema para definir as forças de reação em A e G
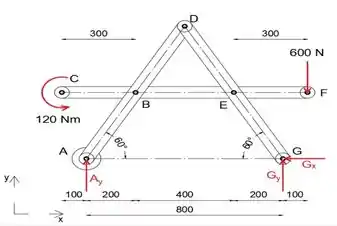
Ao igualar a soma dos momentos sobre o ponto A a zero, podemos determinar a força de reação G
Observe que convertemos o par de 120 Nm em
Ao igualar a soma dos momentos sobre a direção y a zero, podemos determinar a força de reação Ay
Substitua Gy por seu valor
Ao igualar a soma dos momentos sobre a direção x a zero, podemos determinar a força de reação Gx
A seguir, vamos isolar e desenhar o diagrama de corpo livre do membro CF
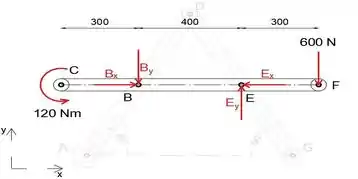
Passo 2
Ao igualar a soma dos momentos sobre o ponto B , podemos determinar a força de reação Ey
Equacionando a soma das forças na direção y a zero, podemos determinar a força By
Substitua por seu valor
Passo 3
Ao igualar a soma das forças na direção x a zero, podemos encontrar a relação entre as forças Bx e Ex
Finalmente, vamos isolar e desenhar o diagrama de corpo livre do membro DEG
Observe que a altura do triângulo △ AGD é:
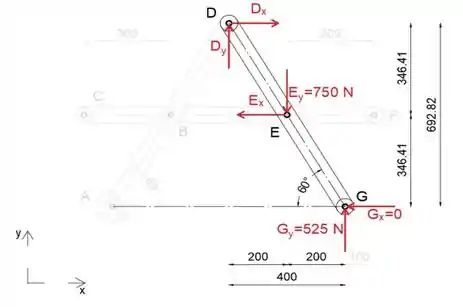
Passo 4
Equacionando a soma dos momentos sobre o ponto D a zero, podemos determinar a força Ex
Substitua Ex por seu valor na equação (1) para determinar a força Bx
Equacionando a soma das forças na direção x a zero, podemos determinar a força Dx
Equacionando a soma das forças na direção y a zero, podemos determinar a força Dy