Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 70

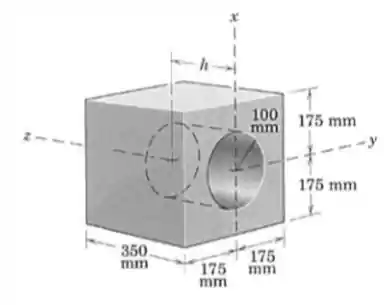
Determine a profundidade h do furo circular no cubo, para a qual a coordenada z do centro de massa terá o maior valor possível.

Passo 1

Questão bem bacana, que vai nos lembrar do que a gente vê lá no cálculo 1... mas calma gente, né nenhuma integral impossível de resolver não! É sobre o assunto de derivadas. Primeiro vamos ao mais básico, as áreas e os centros de massa de cada área! Na verdade, substituiremos as áreas pelos volumes, mas dá no mesmo! Devemos sempre lembrar que as formulas do centro de massa estão a seguir:

X - =   ∑ x - A   ∑ A    

  Y - =   ∑ y - A   ∑ A    

Z - =   ∑ z - A   ∑ A    

Passo 2

Agora, vamos dividir nosso problema em volumes, e a partir dai jogar na nossa formula, substituindo área por volume! A seguir uma vista melhor da figura pra vocês terem uma ideia melhor do que ta rolando!

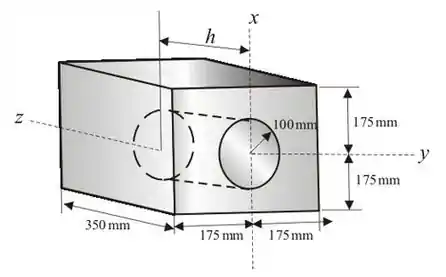
Entenderam a jogada da questão? Ela quer que a gente ache o nosso   Z - mas de forma máxima, ou seja... vamos achar o nosso centro de massa e em seguida derivar!

Passo 3

Vamos calcular o nosso centro de massa no volume 1 (considerando o cubo):

V t o t a l 1 = 350 3 = 42   875   000   m m 3

z - 1 = 175   m m 3

Vamos calcular o nosso centro de massa no volume 2 (considerando o buraco):

V t o t a l 2 = - π 100 2 h

z - 2 = h 2

Passo 4

Agora vamos montar nossa função e deriva-la, pra matar a questão de vez!

Z - =   ∑ z - V   ∑ V = 42   875   000 175 - π 100 2 h h 2   42   875   000 - π 100 2 h

d Z - d h = 42   875   000 - π 100 2 h   - π 100 2 h - 42   875   000 175 - π 100 2 h h 2 42   875   000 - π 100 2 h = 0  

Logo,

h = 187.9   m m

Resposta

h = 187.9   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide do elemento.
Calcule as coordenadas x , y e z do centro de massa do acessório formado a partir de uma placa de alumínio de espessura uniforme.
Determine o volume V gerado girando a área elíptica em 180 ° em torno do eixo z.
Determine o volume V gerado girando a área elíptica em 180 ° em torno do eixo z.
Usando os métodos deste artigo, determine a área de superfície A e o volume V do corpo formado girando a área retangular em 360 em torno do eixo z.