Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 78
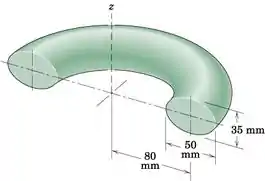
Determine o volume V gerado girando a área elíptica em 180 em torno do eixo z.
Passo 1
Lembre-se dos teoremas de Pappus que a superfície externa de um corpo pode ser encontrada pela fórmula:
E o Volume pode ser encontrado pela fórmula:
Passo 2
Começamos procurando a distância do centro de massa do corpo ao eixo Z. Observe que a linha paralela ao eixo Z que passa pelo centro dos dois eixos da área elíptica é um eixo de simetria, portanto, o centro de massa será encontrado nesse eixo. O mesmo vale para o eixo X. Portanto, o centro será encontrado onde o eixo da elipse se encontra:
Em seguida, precisamos encontrar , uma vez que a revolução é 180, escrevemos:
Em seguida, estamos procurando encontrar o Volume aqui, então usaremos a segunda fórmula do Teorema de Pappus:
Passo 3
A última coisa de que precisamos é a área. Temos uma elipse com
e ,
Então a área é:
Temos tudo o que precisamos para encontrar o Volume, então:
Resposta
Comece encontrando a distância do centro de massa do corpo ao eixo Z. Em seguida, encontre o ângulo de revolução em radianos. O próximo passo é encontrar a área da elipse e finalmente aplicar os teoremas de Pappus