Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 30

Determine a reação no apoio móvel e a deflexão no ponto C .

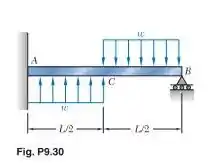
Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Primeiramente, precisamos da equação do momento na estrutura. Teremos duas equações, uma até a metade, e outra no restante. Ou seja:

0 < x < L 2

Agora, com a equação do momento encontrada, basta substituir na equação da linha neutra e integrar duas vezes para acharmos a equação da linha elástica. Logo:

E I d 2 y d x 2 = M A + R A x + 1 2 w x ²

E I d y d x = M A x + 1 2 R A x 2 + 1 6 w x ³ + C 1

E I   y = M A x 2 2 + 1 6 R A x 3 + 1 24 w x 4 + C 1 x + C 2

Agora, faremos o mesmo para a segunda metade da estrutura:

E I d 2 y d x 2 = M A + R A x + 1 2 w L x - L 4 - 1 2 w x - L 2 2  

E I d y d x = M A x + 1 2 R A x ² + 1 4 w L x - L 4 2 - 1 6 w x - L 2 3 + C 3

E I   y = M A x 2 2 + 1 6 R A x ³ + 1 12 w L x - L 4 3 - 1 24 w x - L 2 4 + C 3 x + C 4

Passo 2

Com as equações acima, basta aplicar as condições de contorno. Sabemos que:

x = 0 → d y d x = 0

x = L 2 → y m e t a d e   1 = y m e t a d e   2

x = L 2 → d y d x m e t a d e   1 = d y d x m e t a d e   2

x = 0 → y = 0

x = L → y = 0  

A minha função aqui é ajudar vocês na questão, e não fazer contas. Logo, essa parte será resumida e explicada. Todas as fórmulas acima são dependentes de x ,   logo, basta substituir os valores e igualar aos resultados das condições de contorno. Após isso, teremos algumas equações e poderemos resolver por sistema. Fazendo isso:

C 1 = C 2 = 0

C 3 = 1 192 w L ³

C 4 = - 1 768 w L 4

R B = 17 64 w L

Passo 3

Agora, basta substituir a coordenada do ponto na equação da deflexão para achar a deflexão pedida. Neste caso:

x = L 2

Substituindo:

y c = 1 1024 w L 4 E I

Resposta

R B = 17 64 w L

y c = 1 1024 w L 4 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Supondo que a viga A E é um perfil de aço laminado W 360 x 101 e que M 0 = 310k N m ,L = 2,4 m ,a = 0,5 m e E = 200G P a , determine (a) a equação Da linha elástica para a parte B D e (b) a deflexão n
Para a viga e o carregamento mostrados, determine (a) a equação da linha elástica, (b) a inclinação na extremidade A e (c) a deflexão no ponto médio do vão.
( a ) Determine a localização e o valor da deflexão máxima absoluta em A B entre A e o centro da viga. ( b ) Considerando que a viga A B seja um perfil W 460 × 113 , M 0 = 224k N ∙ m e E = 200G P a ,
Determine a reação em A e desenhe o diagrama do momento fletor para a viga e o carregamento mostrados nas figuras.
Para a viga e o carregamento mostrados nas figuras, determine (a) a equação da linha elástica, (b) a inclinação na extremidade A e (c) a deflexão do ponto C.