Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 26

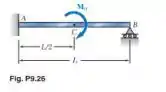
Determine a reação no apoio móvel e desenhe o diagrama de momento fletor para a viga e o carregamento mostrados nas figuras.

Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Primeiramente, precisamos da equação do momento na estrutura. Para isso, vamos aplicar as equações de equilíbrio. Ou seja:

∑ F y = 0

R A + R B = 0

R A = - R B

∑ M A = 0

- M A - M 0 - R B L = 0

M A = R B L - M 0

Agora, vamos determinar a equação do momento. Teremos duas equações, uma até a metade, e outra no restante. Ou seja:

0 < x < 1 2 L

M = R B x + M A = - M 0 + R B L - R B x

Agora, com a equação do momento encontrada, basta substituir na equação da linha neutra e integrar duas vezes para acharmos a equação da linha elástica. Logo:

E I d 2 y d x 2 = M

E I d y d x = - M 0 x + R B L x - 1 2 x + C 1

E I   y = - 1 2 M 0 x 2 + R B 1 2 L x 2 - 1 6 x 3 + C 1 x + C 2

Fazendo o mesmo para a outra metade:

1 2 L < x < L

M = R B L - x

Aplicando a equação da linha neutra:

E I d 2 y d x 2 = M

E I d y d x = R B L x - 1 2 x 2 + C 3

E I   y = R B 1 2 L x 2 - 1 6 x 3 + C 3 x + C 4

Passo 2

Com as equações acima, basta aplicar as condições de contorno. Sabemos que:

x = 0 → d y d x = 0

x = 0 → y = 0

x = L 2 → y m e t a d e   1 = y m e t a d e   2

x = L → y = 0

Agora, basta substituir nas fórmulas para achar as constantes e as reações. Fazendo isso:

C 1 = C 2 = 0

C 3 = - M 0 L 2

C 4 = - 1 8 M 0 L 2 - 1 2 C 3 L

R B = 9 8 M 0 L

M A = - 1 8 M 0

M C = - 7 16 M 0

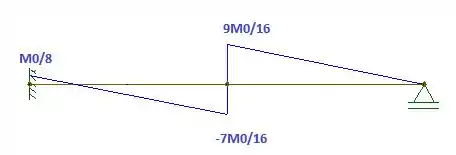
Fazendo o diagrama:

Resposta

R B = 9 8 M 0 L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar:A reação em D
Antes da força P ser aplicada, existe uma abertura δ 0 = 1,9 m m entre as extremidades das barras em balanço A B e C D E . Sabendo-se que E = 200 G P a e P = 3,6k N , determinar:A reação em A
Antes da força P ser aplicada, existe uma abertura δ 0 = 1,9 m m entre as extremidades das barras em balanço A B e C D E . Sabendo-se que E = 200 G P a e P = 3,6k N , determinar:A reação em E
Antes da força P ser aplicada, existe uma abertura δ 0 = 1,9 m m entre as extremidades das barras em balanço A BeC D E . Sabendo-se que E = 200G P a , encontrar a intensidade da força P para que a def
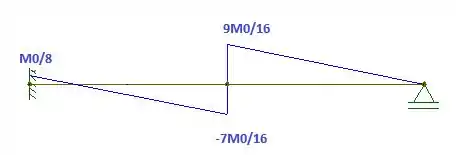
Para a viga com o carregamento mostrado, determinar a intensidade e a localização da maior deflexão. Usar E = 200 G P a .