Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 154
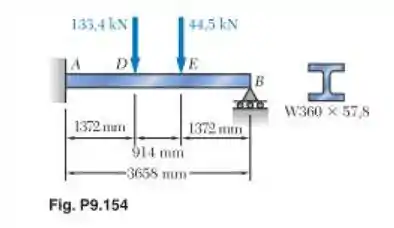
Determine a reação no apoio móvel e trace o diagrama do momento fletor para a viga e o carregamento mostrados na figura.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o método do momento de área. Para isso vamos precisar desenhar o diagrama M/EI para a viga. Depois disso, sabemos que a área entre dois pontos sob a curva M/EI representa a inclinação entre esses dois pontos. E para obter a deflexão, vamos utilizar o teorema do segundo momento de área, que nos fornece o desvio tangencial entre dois pontos. Sabendo disso, temos tudo o que precisamos para resolver o exercício, então bora lá!
Passo 2
Tá legal, vamos começar desenhando o DCL para uma seção da viga de comprimento , orientado da direita para a esquerda, para obter a expressão para o momento nessa parte, então teremos:
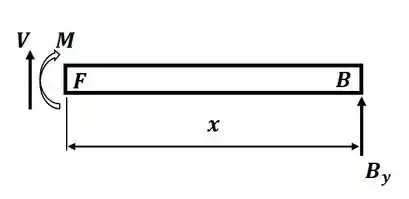
Então, nesse caso, aplicando o somatório de momento em relação ao ponto F, teremos:
Passo 3
Agora, estendendo a seção até algum ponto entre E e D, teremos o seguinte DCL:
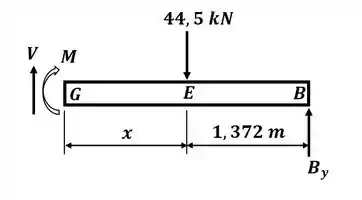
Então, nesse caso, aplicando o somatório de momento em relação ao ponto G, teremos:
Agora, estendendo a seção até algum ponto entre D e A, teremos o seguinte DCL:
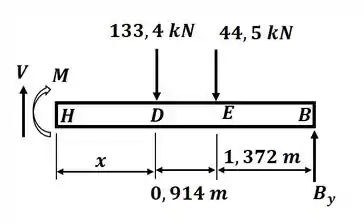
Então, nesse caso, aplicando o somatório de momento em relação ao ponto H, teremos:
Com as equações para o momento que encontramos, podemos dividir o momento em três partes, o momento causado pela reação de apoio em B, que chamaremos de momento 1, o causado pela força localizada em E, que chamaremos de momento 2 e o causado pela força localizada em D, que será o nosso momento 3, então teremos:
Passo 4
Agora vamos calcular os momentos no ponto A para cada um deles, para que depois possamos desenhar o diagrama M/EI, então teremos:
Então nosso diagrama M/EI será:
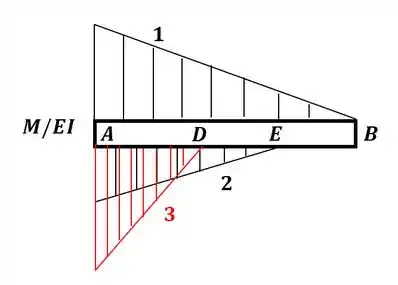
Agora vamos aproveitar e calcular o valor do termo EI, pois precisaremos dele para calcular a área do gráfico que encontramos. Então vamos começar indo lá no apêndice C para pegar o valor do momento de inércia para esse perfil de viga, onde teremos:
Então, considerando E = 200 GPa, o nosso termo EI será:
Passo 5
Então, agora vamos calcular as áreas que encontramos e os seus centroides, então vamos lá:
Passo 6
Agora, para encontrar a reação em B, vamos utilizar o teorema do segundo momento de área entre os pontos B e A, que nos dará:
Substituindo os valores encontrados e sabendo que não teremos deflexão em A e em B por causa do engaste e do apoio, teremos:
Beleza, agora que encontramos a reação no apoio em B, podemos utilizar as equações do momento que encontramos lá no começo para achar as expressões dele em cada uma das seções da viga. Então bora lá.
Passo 7
Pegando a primeira equação, para o trecho , teremos:
Agora, para o trecho , teremos:
E, para a última seção, entre , teremos:
Então, com essas 3 equações, podemos desenhar o diagrama de momento fletor para o nosso caso, que será:
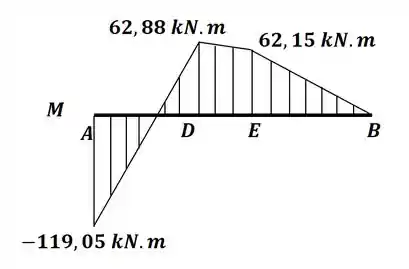
Tooop! Terminamos mais um!!