Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 114

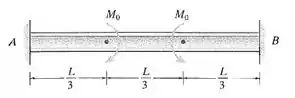
Determine as reações ao momento nos apoios A e B; a seguir trace os diagramas de força cortante e momento fletor. EI é constante.

Passo 1

Fala galera, cá estamos nós novamente para resolver mais um problema de resmat. O primeiro passo é calcular a equação do momento. Logo, caminhando com o x pela viga, teremos:

M x = - M A < x - 0 > 0 + A y < x - 0 > 1 + M 0 < x - L 3 >   0 - M 0 < x - 2 L 3 > 0

O próximo passo é calcular o deslocamento, pela equação da linha neutra. Fazendo isso, teremos:

E I d 2 v d x 2 = M x

Integrando-se duas vezes a equação dos dois lados, ficamos com:

E I v = = - M A x 2 2 + A y x 3 6 + M 0 2 < x - L 3 >   2 - M 0 2 < x - 2 L 3 > 2 + C 1 x + C 2

Para determinarmos as constantes, devemos utilizar algumas condições de contorno:

x = 0 → v = 0   e d v d x = 0

Logo, substituindo, teremos:

C 1 = C 2 = 0

Passo 2

Com a equação do deslocamento completa, precisamos utilizar alguns pontos para acharmos as reações:

x = L → d v d x = 0  

M A = A y L 2 + M 0 3

x = L → v = 0

M A = A y L 3 + M 0 3

Igualando-se as duas equações, temos:

A y = B y = 0

M A = M B = M 0 3

Passo 3

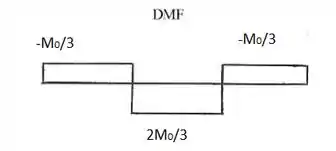
Com as reações calculadas, podemos fazer os diagramas. Como não temos esforço cortante, faremos só o de momento fletor:

Resposta

A y = B y = 0

M A = M B = M 0 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um macaco hidráulico pode ser utilizado para elevar o ponto B da viga em balanço ABC. A viga era originalmente reta, horizontal e sem força aplicada. Foi aplicada então uma força de 20 kN no ponto C,
Determine a reação no apoio móvel e trace o diagrama do momento fletor para a viga e o carregamento mostrados na figura.
Para a viga e o carregamento mostrados na figura, determine a reação em cada apoio.
Para a viga prismática e o carregamento mostrados nas figuras, determine (a) a deflexão no ponto D e (b) a inclinação na extremidade A .
Para a viga o carregamento mostrados na figura, determine ( a ) a inclinação no ponto A e ( b ) a deflexão no ponto D . Use E = 200G P a .