Determine as reações em e . Considere que o apoio em exerce somente um momento sobre a viga. é constante.

Passo 1
Fala aí pessoal, partiu mais um problema de resmat. Este problema pede as reações de apoio e os diagramas. A dificuldade está em encontrar as reações de apoio, pois é uma estrutura hiperestática.
Primeiro, vamos fazer o DCL! Pra isso, vamos substituir a carga distribuída por uma concentrada equivalente.
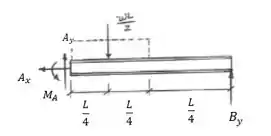
Passo 2
Agora vamos utilizar as equações de equilíbrio e momento para determinarmos as reações:
Passo 3
Agora vamos separar os carregamentos atuando na estrutura, pra poder aplicar o Método da Superposição.
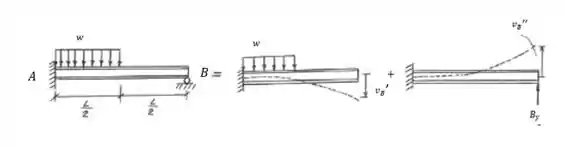
Então vamos usar as fórmulas da Tabela de Deflexão em Vigas (ou Tabela de Deformações e Inclinações). Essa tabela aparece no final de muitos livros. As fórmulas nessa tabela dão pra gente a deflexão em pontos da viga pra diversos carregamentos. A gente vai pegar olha na tabela as deflexões causadas no ponto B por cada carregamento separadamente e somar para encontrar a deflexão total.
Para a carga distribuída em parte de uma viga em balanço, temos a seguinte deflexão:
Para uma carga pontual no extremo que não está engastado, temos uma deflexão:
Cuidado com os sinais. A carga distribuída vai deformar o ponto B pra baixo, por isso a deflexão é negativa. Mas como By deforma a viga pra cima, então a deflexão é positiva. Somando as duas, temos a deflexão total:
Mas tem um detalhezinho aqui muito importante. A gente trocou o apoio em B por uma força By, pra poder usar o Método da Superposição, e olhou na tabela as deflexões pra vigas em balanço. Mas na verdade mesmo, essa viga não está em balanço, ela ta apoiada em um apoio em B. E o apoio impede o movimento vertical. Então essa expressão que a gente achou pra deflexão em B tem que ser nula, porque senão não tem sentido físico!
Passo 4
Substituindo nas equações obtidas anteriormente, encontramos as outras reações de apoio: