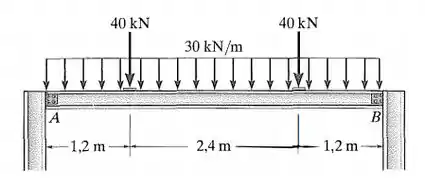
A viga simplesmente apoiada suporta uma carga uniforme de . Em razão do forro de gesso, as restrições determinam que a deflexão máxima não pode ultrapassar do comprimento do vão. Selecione no Apêndice a viga de abas largas de aço A-36 de menor peso que satisfará esse requisito e suportará a carga com segurança. A tensão de flexão admissível é e a tensão de cisalhamento admissível é . Considere que é um pino e é um apoio de rolete.

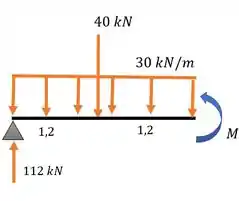
Agora vou te dar um bizu: para vigas biapoiadas, sem balanço e com carregamento simétrico, o momento fletor máximo ocorre no meio da viga e o cortante máximo nas extremidades.

Aí o cortante vai ser a própria reação de apoio:

E o momento a gente pode calcular:

Para escolher a viga na tabelinha, precisamos do , que é esse cara:

Aí a gente vai na tabela. Uma viga que tem um um pouco maior que esse é .

Precisamos testar se ela aguenta o cisalhamento máximo. Vamos usar a expressão de cisalhamento máximo para vigas de abas largas:

Portanto, a tensão de cisalhamento máxima vai ser de:

Podemos observar que este valor é menor do que a tensão admissional de , logo a condição está satisfeita.

Por fim, precisamos chegar se ela atende o critério de deformação máxima. Para a deformação admissível, ela é de:

A deformação máxima vai ocorrer no meio da viga, porque nosso carregamento é simérico.

Para achar esse valor para a nossa viga, a gente vai usar as tabelinhas do fim do livro. Fica assim:

Como monta ela? Ela é a soma de deflexões de vários tipos de viga, que juntas, dão a nossa. O primeiro termo é a fórmula para a deflexão no meio de uma viga biapoiada com carga distribuída , de comprimento .

O segundo é a fórmula para a deflexão em uma viga biapoiada com carga pontual distante do apoio mais próximo e do mais distante. Temos duas cargas nessa situação. Como eslas estão em posições simétricas, podemos só multiplicar o resultado de uma por 2.

Substituindo:

Nota-se que a condição também é satisfeita, pois .