Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 9

Determine a força de cisalhamento máxima V que a escora pode suportar se a tensão de cisalhamento admissível para o material for τ a d m = 40   M P a

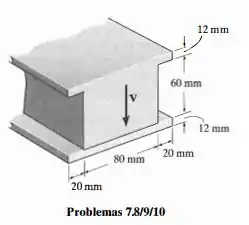
Passo 1

Dados da questão: τ a d m = 40   M P a

A questão pede: A força de cisalhamento aplicada. V = ?

Esta é uma questão bem direta. Sabemos que quanto mais próximo do centroide, maior será a tensão de cisalhamento. Ao mesmo tempo, sabemos que quanto menor a espessura t , maior será a tensão de cisalhamento.

Como o centroide da figura é a região de menor espessura, isso facilita o nosso trabalho! Vamos simplesmente utilizar a Equação 7.3 no centroide e isolar o V . Para aplicar essa equação vamos precisar calcular o Momento de Inércia ( I ) e o Momento Estático ( Q ) . Não será preciso calcular o centroide, pois como a figura é perfeitamente simétrica o centroide fica no centro.

Passo 2

Observe a figura abaixo. Podemos facilmente calcular o momento de inércia da figura, subtraindo o momento de inércia da figura laranja pelas duas figuras verdes.

I = I l a r a n j a - 2 ⋅ I v e r d e

I = 120 ⋅ 84 3 12 - 2 ⋅ 20 ⋅ 60 3 12

I = 5207040   m m 4

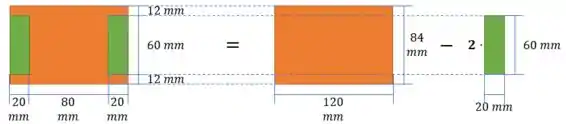
Passo 3

Como queremos a tensão sobre o centroide, basta calcular o momento estático de metade da figura! Observe a figura abaixo, pra calcular o momento estático que nos interessa, basta somar o momento estático da parte azul com o da parte amarela.

Q = Q a z u l + Q a m a r e l a

Q = A a z u l ⋅ y a z u l + A a m a r e l o ⋅ y a m a r e l o

Q = 12 ⋅ 120 ⋅ 36 + 30 ⋅ 80 ⋅ 15

Q = 87840   m m 3

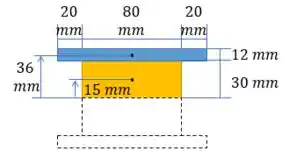
Passo 4

Agora basta aplicar a Equação 7.3

τ = V Q I t

Isolar o esforço cortante:

V = τ ⋅ I ⋅ t Q

Note que pra nossa região de interesse t = 80 m m . Substituíndo os outros valores:

V = 40   M P a ⋅ 5207040   m m 4 ⋅ 80 m m 87840   m m 3

V = 189691,8   M P a ⋅ m m 2 = 189691,8   P a ⋅ m 2

Convertendo as unidades:

V = 189,69   k N

Resposta

V = 189,69   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é feita de um material cerâmico cuja tensão de flexão admissível é σ a d m = 5 MPa e tensão de cisalhamento τ a d m = 2,8 MPa. Determine a largura b da viga, se a altura for h=2b.
Para uma viga feita de dois ou mais materiais diferentes módulos de elasticidade. Mostre que a Equação (6.6) τ m e d = V Q I t permanece válida desde que Q e I sejam calculados usando a seção transfor
Uma placa de 6,35 mm de espessura é enrugada, conforme mostra a figura, e depois usada como uma viga . Para uma força cortante vertical de 5,34 kN, determine (a) a tensão de cisalhamento no ponto B. E
Uma viga extrudada tem a seção transversal mostrada na figura é uma parede de espessura uniforme de 3 ymm. Para força cortante vertical de 10 kN, determine (a) o tensão de cisalhamento no ponto A, (b)