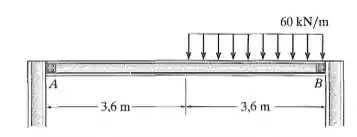
A viga suporta a carga mostrada na figura. Em razão do forro de gesso, as restrições determinam que a deflexão máxima não pode ultrapassar 1/360 do comprimento do vão. Selecione no Apêndice B a viga de abas largas de aço A-36 de menor peso que satisfará esse requisito e suportará a carga com segurança. A tensão de flexão admissível é e a tensão de cisalhamento admissível é . Considere que A é um rolete e B é um pino.

Fala aí galera. Vamos pra mais uma questão de resmat. O problema quer que a gente escolha uma estrutura que seja adequada para a situação. Primeiramente, sabemos que:

Logo, esse é o que chamamos de parâmetro S. Isso é tabelado. Calculando-se o momento máximo, que se encontra no meio da carga distribuída, teremos:

Logo, nosso S será:

Pegando a viga W410,que possui S= , precisamos verificar se ela está de acordo com as tensões e deformações admissíveis. Logo, calculando as tensões e deformações, teremos:

Fazendo o limite de deformação:

Portanto, podemos ver que as tensões e as deformações são menores que as limite.