Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 123
A viga e a haste de aço A-36 são usadas para suportar a carga de . Se for exigido que a tensão normal admissível para o aço seja e a deflexão máxima não ultrapasse , determine o menor diâmetro da haste a ser usado. A viga é retangular, com de altura e de espessura
Passo 1
Fala aí pessoal, partiu mais um problema de resmat. Este problema pede as reações de apoio e os diagramas. A dificuldade está em encontrar as reações de apoio, pois é uma estrutura hiperestática. Primeiro, vamos fazer o DCL:
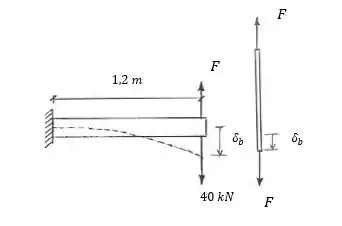
Passo 2
Agora, sabendo que:
Passo 3
Precisamos agora, encontrarmar o momento máxima para conferirmos se a tensão amdissível suportaria, temos:
Passo 4
Por fim, temos:
Com isso, a :
Resposta
Exercícios de Livros Relacionados
Determine as reações nos apoios A e B . E I é constante.
Determine as reações nos apoios de mancal A , B e C do eixo; a seguir, trace os diagramas de força cortante e momento fletor. E I é constante. Cada mancal exerce somente reações verticais sobre o eixo
Determine as reações em A e B . Considere que o apoio em A exerce somente um momento sobre a viga. E I é constante.
Determine a reação nos apoio C . E I é constante para ambas as vigas.
Determine as reações nos apoios A , B e C ; a seguir, trace os diagramas de força cortante e momento fletor. E I é constante.