Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 121

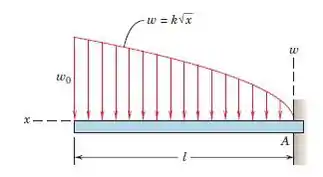
Determine as reações de força e momento no apoio A da viga cantilever submetida à distribuição de carga mostrada.

Passo 1

Podemos efetivamente inverter a carga e definir a origem do eixo para a ponta do cantilever com x correndo positivo em direção a A. A magnitude da carga não muda depois de inverter a carga, mas agora o máximo ocorre no suporte. (Este não é o caso, mas é útil para calcular a posição do centroide). Em seguida, substituímos a carga distribuída por uma força concentrada. Este atua em L-x de A com x o centróide da área sob a curva na configuração invertida.

F = ∫ 0 L   x d x = 2 k 3 L 3

F x - = ∫ 0 L   x ( L - x ) d x = ∫ 0 L   x L - x 3 d x = k 2 3 L 5 - 2 5 L 5

x - = 1 F k 2 3 L 5 - 2 5 L 5 = L - 3 L 5 = 2 L 5

E o momento do braço se torna L

L - 2 L 5 = 3 L 5

Passo 2

R A = F = 2 k 3 L 3

Note que ω o = k L  então  k = ω o L  e  R A = 2 ω o L 3

M A = F × 3 L 5 = R A × 3 L 5 = 2 ω o L 2 5

Resposta

R A = 2 ω o L 3 ; M A = 2 ω o L 2 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o centro de gravidade mostrado na figura, sabendo que ela é feita de barras finas de latão o diâmetro uniforme.
Um colar de broze de comprimento 60m m é montada em barra de aluminio
Uma bucha de bronze é montada na parte inferior de uma luva de aço. Sabendo que o peso específico do bronze é 57240N / m 3 e a do aço é 51120N / m 3 , determine o centro de grávidade do conjunto.
Um cinzel tem um punho de plástico e uma lâmina e haste de aço. Sabendo que a densidade do plástico é 1030k g / m 3 e o do aço é 7860k g / m 3 , determine o centro de gravidade dessa ferramenta.
Uma pequena mesa com tampo de vidro de três pernas igualmente espaçados feitas em tubos de aço com os diâmetro externo é 24m m e área da secção transversal de 150m m 2 . O diâmetro e a espessura do ta